એક પદ્વર્થનો ગ્રહ $'A'$ ઉપર નિષ્કમણવેગ $12 \,kms ^{-1}$ છે. આ પદાર્થનો બીજા ગ્રહ $'B'$ કે જેની ગ્રહ $'B'$ કે જેની ગ્રહ $'A'$ કરતાં ઘનતા ચારગણી અને ત્રિજ્યા અડધી હોય તેના પર નિષ્ક્રમણ વેગ .................. $kms ^{-1}$ થશે.
JEE MAIN 2022, Medium
Download our app for free and get started
a
\(V _{\text {escape }}=\sqrt{\frac{2 Gm }{ R }} \Rightarrow \sqrt{\frac{2 G \rho \times \frac{4}{3} \pi R ^{3}}{ R }}\)
\(V _{\text {escape }}=\sqrt{\frac{2 Gm }{ R }} \Rightarrow \sqrt{\frac{2 G \rho \times \frac{4}{3} \pi R ^{3}}{ R }}\)
\(V _{\text {escape }} \propto \sqrt{\rho R ^{2}}\)
\(\therefore\) if \(\rho\) is \(4\) times and Radius is halved.
\(\Rightarrow V_{\text {escape }}\) will remain same
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $I$ : જો પૃથ્વીની આજુબાજુ ફરતા ઉપગ્રહની કુલ ઊર્જા $E$ હોય તો તેની સ્થિતિ ઊર્જા $\frac{ E }{2}$ હશે.
વિધાન $II$ : કક્ષામાં ગતિ કરતા ઉપગ્રહની ગતિઊર્જા, કુલ ઊર્જા $E$ ના અડધા મૂલ્ય બરાબર છે.
ઉપરોક્ત વિધાનોના આધારે, નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 2પૃથ્વીની સપાટી પરથી શિરોલંબ દિશામાં પદાર્થને અનંત અંતરે પહોચાડવા માટે જરૂરી વેગથી ફેકવામાં આવે છે. તે $h$ ઊંચાઈ સુધી પહોંચવા માટે કેટલો સમય લેશે?View Solution
- 3એક પદાર્થ $M$ દળ અને $R$ ત્રિજ્યા ધરાવતા ગ્રહની ફરતે નીચી વર્તુળાકાર કક્ષામાં ગતિ કરે છે. તેની કક્ષાની ત્રિજ્યાને $R$ પણ લઈ શકાય. તો આ પદાર્થના કક્ષીય વેગ અને આ ગ્રહની નિષ્ક્રમણ ઝડપનો ગુણોત્તર કેટલો થાય?View Solution
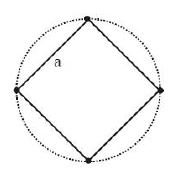
- 4ચાર $M$ દળના કણ $a$ ત્રિજયાના ચોરસના શીરોબિંદુ પર છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે આ કણને બીજા કણોના ગુરુત્વાકર્ષણ ક્ષેત્રને લીધે વર્તુળાકાર કક્ષામાં ભ્રમણ કરતા હોય તો તેનો વેગ કેટલો હશે?View Solution
- 5આ પ્રશ્નો વિધાન $- 1$ અને વિધાન $- 2$ માં છે. ચાર વિકલ્પોમાંથી પસંદ કરવાના રહેશે. તેમાંથી એક સાચો જવાબ પસંદ કરવાના રહેશે.View Solution
વિધાન $-1$ : એક $m$ દળનાં પદાર્થને $a$ બાજુવાળા ધનના કેન્દ્રમાં રાખ્યો છે. ધનની બાજુમાંથી પસાર થતા ગુરત્વાકર્ષી ક્ષેત્રના ફલક્સનું મૂલ્ય $4 \pi GM$ छे.
વિધાન $-2$ : બિંદુવત ઉદગમને કારણે ત્રિજ્યાવર્તી ક્ષેત ઉદ્ભવે છે. જે ઉદગમથી $r$ અંતરે $\frac{1}{ r ^{2}}$ ના સમપ્રમાણમાં હોય છે. ક્ષેત્રનું ફલક્સ ફક્ત ઉદગમ પર આધારિત છે, નહિ કે ઉદ્દગમની આસપાસની સપાટી કे કવચની સાઈઝ અથવા આાકાર પર.
- 6View Solutionઉપગ્રહને પૃથ્વીના ગુરુત્વાકર્ષણ થી મુકત કરવા માટે જરૂરી ગતિઊર્જા અને પૃથ્વીની સપાટી નજીક ભ્રમણ કરવા માટે જરૂરી ગતિઊર્જાનો ગુણોત્તર કેટલો થાય?
- 7કેન્દ્રથી $r$ અંતરે ભ્રમણ કરતા ઉપગ્રહનું કોણીય વેગમાન $L$. છે. તો અંતર વઘારીને $16r$, કરવામાં આવે તો નવુ કોણીય વેગમાન કેટલું થાય?View Solution
- 8View Solutionજો ઉપગ્રહ પૃથ્વી તરફ વળે તો તો તેનો પરિભ્રમણ સમય...
- 9જો પૃથ્વી પોતાની અક્ષને ફરતે ભ્રમણ કરવાનું બંધ કરે તો $45^o$ અક્ષાંશ પર $g$ ના મૂલ્યમાં $C.G.S.$ એકમમાં ........ $cm/sec^{2}$ વધારો થાય.View Solution
- 10View Solutionજો ઉપગ્રહ-ગ્રહ તંત્રની ઊર્જા ધન હોય, તો ઉપગ્રહએ .....