એક પ્રવાહી એક સમક્ષિતિજ નળી કે જેનો આડછેદ બદલાતો હોય તેમાં જે સ્થાને $P$ પાસ્કલ દબાણ હોય ત્યાં $v\;ms^{-1}$ વેગથી વહે છે. બીજા સ્થાને જ્યાં દબાણ $\frac{ P }{2}$ હોય ત્યાં તેનો વેગ $V\;ms^{-1}$ છે. જો પ્રવાહીની ઘનતા $\rho\, kg\, m ^{-3}$ અને પ્રવાહ ધારારેખી હોય તો $V$ કેટલો હશે?
JEE MAIN 2020, Medium
Download our app for free and get started
b
Applying Bernoulli's Equation
Applying Bernoulli's Equation
\(P _{1}+\frac{1}{2} \rho v _{1}^{2}+\rho gy _{1}= P _{2}+\frac{1}{2} \rho v _{2}^{2}+\rho gy _{2}\)
\(P +\frac{1}{2} \rho v ^{2}=\frac{ P }{2}+\frac{1}{2} \rho V ^{2}\)
\(\frac{2 P }{2 \rho}+\frac{1}{2} \frac{\rho v ^{2}}{\rho} \times 2= V ^{2}\)
\(\sqrt{\frac{P}{\rho}+v^{2}}=V\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionપ્રવાહીના વહન માટે બર્નુલીના નિયમનો ઉપયોગ નીચેનામાથી શેમાં થાય છે.
- 2View Solutionસાચું બર્નોલીનું સમીકરણ. . . . . . .છે. (સંજ્ઞાઓ તેમનો પ્રમાણિત અર્થ રજૂ કરે છે.)
- 3બે મોટા હાડકાના આડછેદના ક્ષેત્રફળ $10 \,cm ^2$ છે અને ઉપરનો ભાગ $50 \,kg$. ધરાવતા વ્યક્તિના ઉપરના ભાગ સાથે જોડેલ છે. તો સરેરાશ હાડકા વડે થતું દબાણ ......... $N / m^2$View Solution
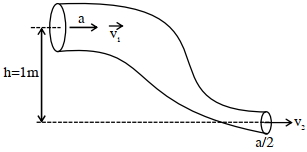
- 4$800 \,kgm ^{-3}$ ઘનતા ઘરાવતું એક આદર્શ પ્રવાહી (આકૃતિમાં દર્શાવ્યા મુજબ) એક વળેલી નળીમાંથી સહેલાઈથી/સરળતાથી વહન પામે છે.આ નળીનો આડછેદ $a$ થી ઘટીને $\frac{a}{2}$ થાય છે. પહોળા અને સાંકળા છેડાઓ વચ્ચે દબાણનો તફાવત $4100 \,Pa$ છે. પહોળા છેડા આગળ પ્રવાહીનો વેગ $\frac{\sqrt{x}}{6} ms ^{-1}$ છે. $x$ નું મૂલ્ય ........ થશે. $\left( g =10 ms ^{-2}\right.$ છે.)View Solution
- 5એક પૂર્ણ રીતે ભરેલા બોઈગ વિમાનનું દળ $5.4 \times 10^5\,kg$ છે. તેની પાંખોનું કુલ ક્ષેત્રફળ $500\,m ^2$ છે. તે $1080\,km / h$ ની ઝડપે લેવલ (સમક્ષિતિજ) ઉડ્ડયન સ્થિતિમાં છે. જો હવાની ધનતા $1.2\,kg m ^{-3}$ હોય તો વિમાનની ઉપરની સપાટી આગળ, તેની નીચેની સપાટીની સરખામણીમાં, હવાની ઝડપમાં પ્રતિશત આાંશિક વધારો $.........$ થશે. $(g=10\;m / s ^2)$View Solution
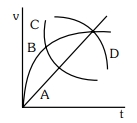
- 6એક ગોળાકાર બોલને ખુબજ સ્નિગ્ધ પ્રવાહીના લાંબા સ્તંભમાં મુક્ત (છોડવામાં)કરવામાં આવે છે.આકૃતિમાં દર્શાવેલ વક્ર,કે જે બોલ માટે ઝડપ $(v)$ અને સમય $(t)$ના વિધેય તરીકે દર્શાવે તે$........$છે.View Solution
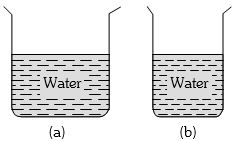
- 7View Solutionઆકૃતિ પરથી નીચેનામાંથી સાચું વિધાન કયું છે?
- 8પાત્રના તળિયે $ l $ લંબાઇ અને $r $ ત્રિજયા ઘરાવતી કેશનળી જોડેલ છે.તેના પર દબાણનો તફાવત $P$ હોય,ત્યારે બહાર આવતા પાણીનું કદ $ V$ છે,હવે તેની સાથે શ્રેણીમાં સમાન લંબાઇ પરંતુ અડધી ત્રિજયા ધરાવતી કેશનળી જોડતાં બહાર આવતાં પ્રવાહીનું કદ કેટલું થાય? ( તંત્ર વચ્ચે દબાણનો તફાવત $P$ છે. )View Solution
- 9$\sigma$ સાપેક્ષ ધનતા ધરાવતા એક ગોળાનો વ્યાસ $D$ છે અને તેને $d$ વ્યાસનો સમકેન્દ્રિય પોલાણ઼ (ખાડો) છે. જો તે ટેન્કમાંના પાણી પર તરી શકે તે માટે $\frac{\mathrm{D}}{\mathrm{d}}$ ગુણોત્તર ............ છે.View Solution
- 10એક્ એરોપ્લેન ઉડ્યન સ્તરે અચળ ઝડપે રહેલ છે અને તેની બે પાંખોમાં દરેકનું ક્ષેત્રફળ $40 \mathrm{~m}^2$ છે. જો તેની નીચેની પાંખની સપાટી પર હવાની ઝડ૫ $180 \mathrm{~km} / \mathrm{h}$ અને ઉપરની સપાટી પર $252 \mathrm{~km} / \mathrm{h}$ હોય તો પ્લેનનું દળ_________$kg$છે. (હવાની ઘનતા $1 \mathrm{~kg} \mathrm{~m}^{-3}$ અને $10 \mathrm{~ms}^{-2}$ લો.)View Solution