એક $R$ ત્રિજ્યાનો લીસો ગોળો એક સુરેખ રેખા પર અચળ પ્રવેશ $a = g$ થી ગતિ કરે છે. એક કણને ગોળાના ઉપરના ભાગમાં રાખેલો છે. તેને ત્યાંથી ગોળાની સાપેક્ષે શૂન્ય વેગથી મુક્ત (છોડવામાં) કરવામાં આવે છે. કણ સરકે છે તે દરમિયાન ખૂણા $\theta$ ના વિધેયમાં ગોળાની સાપેક્ષે તેની ઝડપ કેટલી હશે?
Diffcult
d
A force \(f\) acts on the sphere towards left, so the particle experience pseudo force \(f =\) ma towards right.
A force \(f\) acts on the sphere towards left, so the particle experience pseudo force \(f =\) ma towards right.
Initial kinetic energy of the particle is zero.
Let the speed of the particle at point \(C\) be \(v\).
From work-energy theorem, \(W _{ g }+ W _{ f }=\Delta K \cdot E = K \cdot E _{ f }\)
where \(W _{ g }\) is work done by gravity and \(W _{ f }\) is work done by pseudo force.
From figure, we get \(AB = R - R \cos \theta= R (1-\cos \theta)\)
Also \(AC = R \sin \theta\)
\(\therefore mg ( AB )+ f ( AC )=\frac{1}{2} mv ^2\)
Or \(m g R(1-\cos \theta)+(m a)(R \sin \theta)=\frac{1}{2}{m v^2}^2\)
Or \(m g R(1+\sin \theta-\cos \theta)=\frac{1}{2}{m v^2}^2 \quad(\because a=g)\)
\(\Rightarrow v =\sqrt{2 gR (1+\sin \theta-\cos \theta)}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
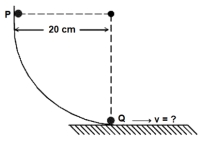
- 1આપેલ આકૃતિ મુજબ, એક નાનો બોલ $P$ વર્તુળના ચોથાભાગ પર સરકીને તેના જેટલું જ સાલ ધરાવતા બીજા બોલ $Q$ને અથડાય છે, કે જે પ્રારંભમાં વિરામ સ્થિતિમાં છે. ઘર્ષણની અસર અવગણતા અને સંઘાત સ્થિતિસ્થાપક છે તેમ ધારતા, $Q$ બોલનો સંઘાતબાદ વેગ $..........$ હશે. $\left( g =10\,m / s ^2\right)$View Solution
- 2એક ટ્યૂબવેલ પંપ પ્રતિ મિનિટે $2400 \;kg$ પાણી બહાર કાઢે છે. જો બહાર આવતાં પાણીની ઝડપ $3\; m/s$ હોય તો, જો પંપ $10$ કલાક ચાલે તો થતું કાર્ય કેટલું હશે?View Solution
- 3દોરડા વડે બાંધેલ બ્લોક પર $4500 N $ નું બળ લગાડીને $2 m/sec$ ના વેગથી ગતિ કરાવવા માટે કેટલા પાવરની જરૂર પડે?View Solution
- 4એક ગાડીને $10 m/s$ થી $20 m/s $ સુધી પ્રવેગી કરવા માટે જરૂરી ઊર્જાએ સ્થિર સ્થિતિએ રહેલી ગાડીને $10 m/s$ જેટલી પ્રવેગીત કરવા માટે જરૂરી ઊર્જા કેટલા ગણી છે?View Solution
- 5લીસા બરફની પાટ રાખેલા $M$ દળના પ્લેટ પર $m$ દળનો માણસ ઊભો છે. જો માણસ પ્લેટફોર્મની સાપેક્ષે $v$ ઝડપ સાથે પ્લેટફોર્મ પર ગતિ કરવાનું શરૂ કરે તો પ્લેટ ફોર્મ બરફની સાપેક્ષે કેટલા વેગથી પાછો ખસે છે?View Solution
- 6$10,000 $ દળની એક ટ્રક $1m$ ઢાળ અને $50 m$ ઉંચાઈ વાળા ઢોળાવના સમતલ પર ચઢાણ કરી રહી છે. જેની ઝડપ $36 km/hr $ છે. એન્જિનનો પાવર.....$kW$ શોધો.($g = 10 m/s^2$)View Solution
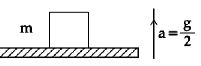
- 7આકૃતિમાં દર્શાવ્યા મુજબ, એક $m$ દળ ધરાવતુ ચોસલું કે જે તેની સ્થિર સ્થિતિમાંથી અચળ પ્રવેગ $g/2$ થી ઊપરની દિશામાં ગતિ શરૂ કરે તેમ રાખેલ છે.$t$ સમયમાં લંબ પ્રત્યાઘાત (normal reaction) દ્વારા કેટલું કાર્ય થશે?View Solution
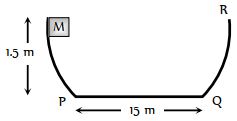
- 8$M $ દળનો પદાર્થ મુકત કરતાં $P$ થી કેટલા ........$m$ અંતરે સ્થિર થશે?પદાર્થ અને સમક્ષિતિજ સપાટી વચ્ચે ઘર્ષણાક $0.2$ છેView Solution
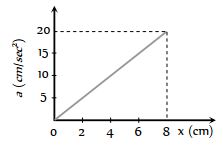
- 9$10 kg$ કણનો પ્રવેગ વિરુધ્ધ સ્થાનનો આલેખ આપેલ છે.તો$x = 0$ cm થી $x = 8$$cm$ થતું કાર્યView Solution
- 10$2kg$ ના પદાર્થનો વેગ $36km/h$ છે. $3kg$ ના સ્થિર રહેલા પદાર્થ સાથે અસ્થિતિસ્થાપક સંધાત થાય,તો ગતિઊર્જામાં થતો ઘટાડો.....$J$View Solution
