એક રેડિયો-ઍક્ટિવ તત્વ માટે સરેરાશ જીવનકાળ છે. $ t = 0$ સમયે તેના એકમ સમયમાં વિભંજન પામતાં ન્યુક્લિયસોની સંખ્યો $n$ છે, તો $0$ અને $t$ સમયની વચ્ચે વિભંજન ન્યુક્લિયસોની સંખ્યા ........ છે.
Medium
c
અહીં, આપેલ રેડિયો-ઍક્ટિવ તત્વ માટે \(t = 0\) સમયે એકમ સમયમાં વિભંજન પામતાં ન્યુક્લિયસોની સંખ્યા \( 'n' \) આપેલ છે. અર્થાત ઍક્ટિવિટી \( I_0 = n \) આપેલ છે.
અહીં, આપેલ રેડિયો-ઍક્ટિવ તત્વ માટે \(t = 0\) સમયે એકમ સમયમાં વિભંજન પામતાં ન્યુક્લિયસોની સંખ્યા \( 'n' \) આપેલ છે. અર્થાત ઍક્ટિવિટી \( I_0 = n \) આપેલ છે.
\(→\) હવે \( t = 0 \) થી \( t = t \) સમયની વચ્ચે વિભજન પામતાં ન્યુક્લિયસોની સંખ્યા \(= N_0 - N\)
પણ \(I_0 = \lambda N_0\) અને \(I =\lambda N \) હોવાથી વિભંજન પામતાં ન્યુક્લિયસોની જરૂરી સંખ્યા
\( = \frac{{{I_0}}}{\lambda } = \frac{I}{\lambda }\, = \frac{{{I_0}}}{\lambda } - \frac{{{I_0}{e^{ - \lambda t}}}}{\lambda }\)
\(= \frac{{{I_0}}}{\lambda }(1 - {e^{ - \lambda t}})\,\)
\(\, = \frac{n}{\lambda }(1 - {e^{ - \lambda t}})\)
\(= n\tau \left( {1 - {e^{ - \frac{t}{\tau }}}} \right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો ન્યુક્લિયર સંલયન પ્રક્રિયામાં પ્રક્રિયક ન્યુક્લિયસનું દળ $m_1$ અને $m_2$ છે. અને પરિણામી ન્યુક્લિયસનું દળ $m_3$ હોય ત્યારે.....View Solution
- 2View Solutionપરમાણુનું કદ એ ન્યુક્લિયસના કદથી કેટલા ગુણાંકમાં વધુ હોય?
- 3${ }_{82}^{290} X \xrightarrow{\alpha} Y \xrightarrow{e^{+}} Z \xrightarrow{\beta^{-}} P \xrightarrow{e^{-}} Q$View Solution
ઉપરોક્ત દર્શાવેલ ન્યુક્લિયર ઉત્સજર્નમાં, $Q$ નીપજનોં દળ ક્રમાંક અને પરમાણુ ક્રમાંક અનુક્રમે. . . . .છે
- 4દ્રાવણમાં રેડિયોએક્ટિવ ${}_{27}^{60}Co$ છે જેની એક્ટિવિટી $0.8\,\mu Ci$ અને વિભંજન અચળાંક $\lambda $ છે, તેને એક પ્રાણીના શરીરમાં ઈંજેક્ટ કરવામાં આવે છે. ઈંજેકશનના $10$ કલાક પછી પ્રાણીના શરીરમાંથી $1 \,cm^3$ રુધિર લેવામાં આવે તો તેમાં વિભંજન દર $300$ વિભંજન પ્રતિ મિનિટ જોવા મળે છે. તો પ્રાણીના શરીરમાં લગભગ કેટલા લિટર રુધિર હશે?View Solution
($1\;Ci = 3.7 \times 10^{10}$ વિભંજન/સેકન્ડ અને $t = 10\, hrs$ સમયે ${e^{ - \lambda t}} = 0.84$)
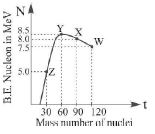
- 5ન્યુક્લિયોન દીઠ બંધન ઊર્જા વિરુદ્ધ પરમાણુદળાંક નો આલેખ આપેલ છે. $W, X, Y$ અને $Z$ ન્યુક્લિયસ ના સ્થાન આપેલા છે. તો કઈ પ્રક્રિયા માં ઊર્જા મુક્ત થાય.View Solution
- 6View Solutionનીચેનામાંથી કયો ન્યુક્લિઅસ આઈસોટોનની જોડ દર્શાવે છે?
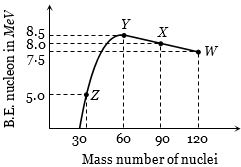
- 7ન્યુકિલયોન દીઠ બંઘન ઊર્જા $ {B_N} $ વિરુધ્ધ પરમાણુભાર $A$ નો આલેખ આપેલ છે,તો કઇ પ્રક્રિયામાં ઊર્જા મુકત થશે?View Solution
- 8એક રેડિયો એકટિવ ઉદગમમાંથી ઉત્સર્જતા $\beta$ કણ માટેનો ઊર્જા વર્ણપટ નીચેનાં પૈકી ક્યો છે? (જ્યાં $N(E)$ એ $\beta$ કણની ઊર્જા $E$ નું વિધેય છે)View Solution
- 9View Solutionજો ઇલેકટ્રૉન અને પોઝિટ્રૉન સંલગ્ન (ભેગા) થાય, તો મુક્ત થતી ઊર્જા ........
- 10View Solutionન્યુકિલયોન દીઠ બંધન ઊર્જા મહતમ કોની હોય?
