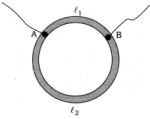
ધારો કે \(x\) એ એકમ લંબાઈ દીઠ અવરોધે છે.
તો સમતુલ્ય અવરોધ \(R = \,\,\frac{{{R_1}{R_2}}}{{{R_1}\, + \,{R_2}}}\)
\( \Rightarrow \,\frac{8}{3}\,\, = \,\,\frac{{(x{{l}_1})\,(x{{l}_2})}}{{x{{l}_1}\, + \,x{{l}_2}}}\)
\( \Rightarrow \,\frac{8}{3}\,\, = \,\,x\,\frac{{{{l}_1}\,{{l}_2}}}{{{{l}_1}\, + \,{{l}_2}}}\)
\( \Rightarrow \,\frac{8}{3}\,\, = \,\,x\,\frac{{{{l}_1}}}{{\frac{{{{l}_1}}}{{{{l}_2}}}\, + \,1}}......(1)\)
અને \({R_0}\,\, = \,x{{l}_1}\, + \,x{{l}_2}\,\) \( \Rightarrow \,12\,\,\, = \,\,x\,({{l}_1}\, + \,{{l}_2})\)
\( \Rightarrow \,\,12\,\, = x{{l}_2}\,\left( {\frac{{{{l}_1}}}{{{{l}_2}}}\, + \,1} \right).....(2)\)
સમીકરણ \({\text{(1)}}\) અને \({\text{(2)}}\) નો ગુણોતર લેતા;
\(\,\frac{{\frac{8}{3}}}{{\frac{{12}}{1}}}\,\,\, = \,\,\frac{{\frac{{x{{l}_1}}}{{\left( {\frac{{{{l}_1}}}{{{{l}_2}}}\, + \,1} \right)}}}}{{x{l_2}\,\left( {\frac{{{{l}_1}}}{{{{l}_2}}}\, + \,1} \right)}}\,\, = \,\,\frac{{{{l}_1}}}{{{l_2}\,{{\left( {\frac{{{{l}_1}}}{{{{l}_2}}}\, + \,1} \right)}^2}}}\)
\( \Rightarrow \,{\left( {\frac{{{{l}_1}}}{{{{l}_2}}}\, + \,1} \right)^2}\, \times \,\frac{8}{{36}}\,\, = \,\,\frac{{{{l}_1}}}{{{{l}_2}}}\)
\( \Rightarrow \,({y^2}\, + \,1\, + \,2y)\, \times \,\frac{8}{{36}}\,\, = \,\,y\,\) [ જ્યા \({y\,\, = \,\,\frac{{{{l}_1}}}{{{{l}_2}}}\,}\)]
\( \Rightarrow \,8{y^2}\, + \,8\, + \,16y\,\, = \,\,36y\)
\( \Rightarrow \,8{y^2}\, + \,8\, + \,16y\,\, = \,\,36y\)
\( \Rightarrow \,8{y^2}\, - \,20y\, + \,8\,\, = \,\,0\)
સમીકરણ ઉકેલતા \({\text{y = 1/2 }}\) અથવા \(\,{\text{2}}\)
\(\,\therefore \,y\,\, = \,\,\frac{{{{l}_1}}}{{{{l}_2}}}\,\, = \,\,\frac{1}{2}\) અથવા \({\text{2}}\)
Download our appand get started for free
Similar Questions
- 1નીચે બે કથનો આપેલા છેView Solution
કથન $I:$ અવરોધોના શ્રેણી સંયોજનનો સમતુલ્ય અવરોધ સંયોજનમાં વપરાતા ન્યૂનત્તમ અવરોધ કરતા નાનો હોય છે.
કથન $II:$ દ્રવ્યની અવરોધકતા તાપમાનથી સ્વતંત્ર છે.
ઉપર્યુક્ત કથનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 2વાહકમાંથી $2\ A$ નો વિધુત પ્રવાહ પસાર કરતાં તેમાં $80\ J$ ની જેટલી ઉષ્મા $10\ seconds$ માં ઉત્પન્ન થાયછે તો વાહકનો અવરોધ ........... $\Omega$ હશે.View Solution
- 3વિદ્યાર્થી કોષના (જેનું $e.m.f.$ $\varepsilon $ છે અને આંતરિક અવરોધ $r$ છે) ટર્મિનલનો સ્થિતિમાનનો તફાવત $(V)$ નો તેમાંથી પસાર થતાં પ્રવાહ $(I)$ સાથેનો સંબંધ માપે છે. $V$ અને $I$ વચ્ચેના આલેખનો ઢાળ અને આંતરછેદ અનુક્રમે શું થાય?View Solution
- 4બે શહેર વચ્ચેનું અંતર $150\, km $ છે. બંને વચ્ચે વિદ્યુતપાવર તાંબાના તાર દ્વારા એકથી બીજા શહેર સુધી મોકલવામાં આવે છે. પ્રતિ $km$ દીઠ સ્થિતિમાનમાં $8 \,V$ નો ધટાડો અને કિલોમીટર દીઠ સરેરાશ અવરોધ $0.5\,\Omega$ છે. તારમાં પાવરનો વ્યય કેટલો હશે?View Solution
- 5$50\,\Omega $ અને $100\,\Omega $ ના અવરોધને શ્રેણીમાં જોડીને $2.4\, V$ ની બેટરી સાથે જોડવામાં આવે છે.$100\, Ω $ ના વોલ્ટમીટરને $100\,Ω$ અવરોધ સાથે જોડતાં વોલ્ટમીટરનું અવલોકન કેટલા ........... $V$ થાય?View Solution
- 6$e.m.f.\,\ E$ અને $r$ આંતરિક અવરોધ વાળા બે કોષ અવરોધ $R$ ના બે છેડે સમાંતરમાં જોડેલા છે. જો અવરોધમાનો પાવર મહત્તમ હોય તો...View Solution
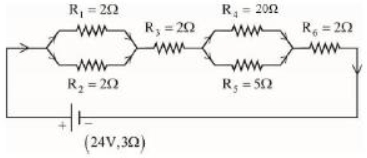
- 7આકૃતિમાં દર્શાવ્યા પ્રમાણે અવરોધોના જાળતંત્રને $3\,\Omega$ આંતરિક અવરોધ ધરાવતી $24\,V$ ની બેટરી સાથે જોડેલ છે. અવરોધો $R _4$ અને $R _5$ માંથી વહેતા વીજ પ્રવાહ અનુક્રમે $I _4$ અને $I _5$ છે. તો $I _4$ અને $I _5$ ના મૂલ્યો શું થાય ?View Solution
- 8એક તારમાંથી વહેતો વિધુતપ્રવાહ સમય સાથે $I = 3t^2 + 2t + 5$ સૂત્ર પ્રમાણે બદલાય છે, તો તારના કોઇ આડછેદમાંથી $t = 0$ થી $t = 2$ સેકન્ડના ગાળામાં પસાર થતો વિધુતભાર ........... $C$ થાય.View Solution
- 9જ્યારે સમાન આડછેદ $a$ લંબાઈ $ℓ$ અને અવરોધ $R$ વાળા તારને સંપૂર્ણ વર્તૂળાકારે વાળ્યો છે. કોઈ પણ બે વિરૂદ્ધ બિંદુઓ વચ્ચેનો અવરોધ .......હશે.View Solution
- 10$25\,W -220\,V$ અને $100\,W -220\,V$ નાં બે વિદ્યુત ગોળાઓ એક $440$ $ V$ નાં સપ્લાય સાથે શ્રેણીમાં જોડેલા છે ................ $W$ વિદ્યુત ગોળો ફયુઝ થશે?View Solution
