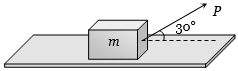
એક રોકેટ ને $2\,g$ પ્રવેગ થી પૃથ્વીથી શિરોલંબ છોડવામાં આવે છે. જ્યાં $g$ એ ગુરુત્વપ્રવેગ છે. રોકેટની અંદર સમક્ષિતિજ થી $\theta $ નો ખૂણો બનાવીને એક ઢોળાવવાળા સમતલ પર $m$ દળ નો પદાર્થ મૂકેલો છે. પદાર્થ ગતિમાન ન થાય તે માટે પદાર્થ અને સમતલ વચ્ચે નો ન્યુનત્તમ ઘર્ષણાંક કેટલો થાય?
JEE MAIN 2016, Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક બીજાથી $1.5 \mathrm{~m}$ દૂર રહેલા બે પાટાઓ પર એક ટ્રેન $12 \mathrm{~m} / \mathrm{s}$ ની ઝડપે ગતિ કરે છે. $400 \mathrm{~m}$ ત્રિજયાનો વક્ર સલામત બને તે માટે બહારના પાટાની અંદરના પાટાની સાપેક્ષ ઉંચાઈ_____ $\mathrm{cm}$ વધારવી પડે. ( $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ આપેલ છે.) :View Solution
- 2$30^o$ ખૂણાવાળા ઢાળ પર $ 5\, kg$ નો બ્લોક મૂકતાં તે અચળ વેગથી ગતિની શરૂઆત કરતો હોય,તો ગતિક ઘર્ષણાંક કેટલો થાય?View Solution
- 3રફ સપાટી પર પડેલ $64 \,N$ ના બ્લોકને ગતિ માટે જરૂરી બળ આપવામાં આવે છે.બ્લોક ગતિમાં આવ્યા પછી પણ આ બળ લગાવવાનું શરૂ રાખવામાં આવે,તો તે કેટલો પ્રવેગ પ્રાપ્ત કરશે? બ્લોક અને સપાટી વચ્ચેનો સ્થિત અને ગતિક ઘર્ષણાંક અનુક્રમે $0.6$ અને $0.4$ છેView Solution
- 4ઢાળ પર પદાર્થ ને ઉપર ખસેડવા લગાવવું પડતું બળ તેને નીચે ખસેડતા અટકાવવા લગાવતા બળ કરતાં બમણું છે. જો ઘર્ષણાંક $0.25$ હોય તો ઢાળ નો ખૂણો ...... $^o$ હશે.View Solution
- 5$800 \mathrm{~kg}$ ની એક કાર $300 \mathrm{~m}$ ની ત્રિજ્યાં અને $30^{\circ}$ ના કોણવાળા ઢોળાવ વાળા રોડ ઉપર વળાંક લે છે. જો સ્થિતિ ઘર્ષણાંક $0.2$ હોય તો સુરક્ષિત રીતે ગાડી આ વળાંક લઈ શકે તે માટે મહત્તમ ઝડપ . . . . .હશે. $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2, \sqrt{3}=1.73\right)$ લો.View Solution
- 6એક કાર $40\,m$ ત્રિજ્યા ધરાવતા વર્તુળાકાર સમક્ષિતિજ રસ્તા ઉપર $20\,m / s$ ની અચળ ઝડપે ગતિ કરે છે. એક દોલકને કારની છત ઉપરથી દળરહિત દોરી વડે લટકાવવામાં આવે છે. શિરોલંબ સાથે દોરીએ બનાવેલો કોણ $............$ થશે. ( $g =10\,m / s ^2$ લો.)View Solution
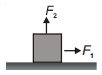
- 7આકૃતિમાં દર્શાવ્યા પ્રમાણે, બળ $F_1$ ને એક બ્લોક પર લગાડવામાં આવે છે તો પણ બ્લોક ગતિ કરતો નથી. ત્યારબાદ શિરોલંબ દિશામાનાં બળ $F_2$ ને શૂન્યથી વધારવામાં આવે છે તો બ્લોક ગતિ કરવાનું શરુ કરે છે તો; સાયું નિવેદન ક્યું છેView Solution
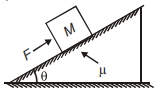
- 8એક બ્લોક દળ = $M \,kg $ ને એક ખરબચડી ઢોળાવવાળી સમતલ પર મુકવામાં આવે છે. એક બળ $F$ ને ઢાળની સમાંતર એવી રીતે લગાડવામાં આવે છે (આકૃતિમાં દર્શાવ્યા મુજબ) જેથી બ્લોક ઉર્ધ્વ દિશામાં તરત જ ગતિ કરે છે. તો $F$ નું મૂલ્ય કેટલું છેView Solution
- 9View Solutionટેબલ પર ચેઇનની ત્રીજા ભાગની લંબાઇ લટકાવી શકાતી હોય,તો ચેઇન અને ટેબલ વચ્ચેનો ઘર્ષણાંક કેટલો હશે?
- 10બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $\mu$ હોય તો બ્લોક અને સપાટી વચ્ચે કેટલું ઘર્ષણ બળ લાગતું હશે?View Solution
