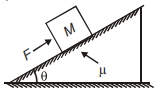
એક બ્લોક દળ = $M \,kg $ ને એક ખરબચડી ઢોળાવવાળી સમતલ પર મુકવામાં આવે છે. એક બળ $F$ ને ઢાળની સમાંતર એવી રીતે લગાડવામાં આવે છે (આકૃતિમાં દર્શાવ્યા મુજબ) જેથી બ્લોક ઉર્ધ્વ દિશામાં તરત જ ગતિ કરે છે. તો $F$ નું મૂલ્ય કેટલું છે
Easy
Download our app for free and get started
b
(b)
(b)
\(F\) will oppose friction force and gravitation force
\(F=m g \sin \theta+\mu m g \cos \theta\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો કોઈ બ્લોક $5 \,m / s$.ના વેગ સાથે $30^{\circ}$ ઢોળાવવાળી સપાટી ૫ર ઊધ્વદિશામાં ગતિ કરે છે, તે $0.5 \,s$ પછી અટકી જાય છે, તો પછી ઘર્ષણાંક લગભગ કેટલું હશે ?View Solution
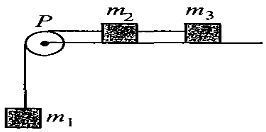
- 2$m_1,m_2$ અને $m_3$ દળવાળા ત્રણ બ્લોકનું બનેલું તંત્ર ગરગડી $P$ પરથી પસાર થતી દોરી સાથે બાંધેલું છે. $m_1$ દળ મુકત રીતે લટકાવેલો છે અને $m_2$ તથા $m_3$ એક રફ સપાટીવાળા સમક્ષિતિજ ટેબલ (જેનો ઘર્ષણાંક $\mu $ છે) પર છે. ગરગડી ઘર્ષણરહિત અને તેનું દળ અવગણ્ય છે. જો $m_1=m_2=m_3=m$ હોય, તો $m_1$ નો નીચેની દિશામાં પ્રવેગ કેટલો હશે?View Solution
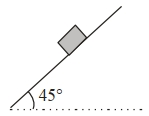
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે ઢળતા સમતલ પર ($45^{\circ}$ પર ઢળતા) બ્લોકને ધ્યાનમાં લો. જો ઢાળ પર ઉપરની તરફ ધકેલવા માટેનું બળ તેને સરકતો અટકાવવા માટેના બળ કરતાં બમણું હોય તો બ્લોક અને ઢાળના સમતલ વચ્યેનો ધર્ષણાંક $(\mu)$ બરાબર $.......$ હોય.View Solution
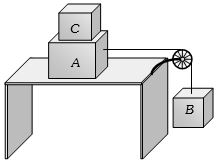
- 4$A$ અને $B$ ના દળ $10\,kg$ અને $5\,kg$ છે,$A$ અને ટેબલ વચ્ચેનો ઘર્ષણાક $0.2$ છે.$C$ નું લઘુત્તમ દળ ....... $kg$ હોવું જોઈએ કે જેથી $A$ ખસે નહિ.View Solution
- 5View Solutionમહત્તમ સ્થિર ઘર્ષણ બળ
- 6$A$ અને $B$ બ્લોકના દળ અનુક્રમે $m$ અને $M$ છે.$A$ અને $B$ વચ્ચે અચળ ઘર્ષણ બળ $F$ છે અને $B$ એ સરળ સમક્ષિતિજ સપાટી પર લપસી શકે છે.$B$ સ્થિર હોય ત્યારે $A$ ને વેગથી ગતિ આપવામાં આવે છે. જ્યારે બંને સમાન વેગથી ગતિ કરે ત્યારે $B$ ની સાપેક્ષમાં $A$ દ્વારા કપાયેલ અંતર .......View Solution
- 7$60\, kg$ નો માણસ થાંભલા પર $600 \,N$ બળ લગાવીને નીચે ઉતરે છે.હાથ અને થાંભલા વચ્ચેનો ઘર્ષણાંક $0.5$ હોય,તો માણસ ........ $m/s^2$ પ્રવેગ પ્રાપ્ત કરશે. $(g = 10\,\,m/{s^2})$View Solution
- 8View Solutionસમક્ષિતિજ રસ્તા પર થતી કારની પ્રવેગી ગતિ શાને આભારી છે
- 9$1\; m$ ત્રિજ્યાના એક પોલા નળાકાર પીપડાની અંદરની સપાટીના સંપર્કમાં $10 \;kg$ દ્રવ્યમાનનો એક બ્લોક છે. આ બ્લોક અને નળાકારની અંદરની સપાટી વચ્ચેનો ઘર્ષણાંક $0.1$ છે. જ્યારે આ નળાકાર શિરોલંબ હોય અને તેની અક્ષને સાપેક્ષે ફરતો હોય ત્યારે આ બ્લોકને સ્થિર રાખવા કેટલા કોણીય વેગની ($rad/s$ માં) જરૂર પડે? $(g = 10\,m/{s^2})$View Solution
- 10View Solutionજ્યારે સાઇકલ ગતિમાં હોય ત્યારે સપાટી દ્વારા બંને પૈડાં પર લાગતું ઘર્ષણબળ કઈ રીતે કામ કરે ?