ધારો કે અંતઃર્ગોળ અરીસાથી મૂકેલી વસ્તુનું અંતર \(= x\) છે. સમતલ અરીસાની વસ્તુનું અંતર \(= (22.5 - x)\)
અંતે સમતલ અરીસો અરીસાની પાછળ \((22.5 - x)\) અંતરે વસ્તુનું પ્રતિબિંબ સમાન અને ચત્તું રચશે.
કેમકે અંતઃર્ગોળ અરીસા વડે રચાતુ પ્રતિબિંબ સમતલ અરીસા વડે રચાતા પ્રતિબિંબ સાથે સંપાત થાય છે.
\(v = - [22.5 + (22.5 - x)] = - (45 - x)\) અને \(u = - x\)
\(\therefore \,\,\,\frac{1}{{ - (45 - x)}}\,\, + \,\,\,\frac{1}{{ - x}}\,\, = \,\,\frac{1}{{ - 10}}\,\,\,\, \Rightarrow \,\,\,\,\frac{{45}}{{(45\,x - {x^2})}}\,\, = \,\,\,\frac{1}{{10}}\)
\(i.e.,\,\, x^{2} - 45x + 450 = 0 \)
\((x - 30) (x - 15) = 0\)
\(i.e.,\,\, x = 30\,\, cm\) અથવા \( x = 15 \,\, cm\) બે અરીસા વચ્ચેનું અંતર \( = 22 \,\, cm\) તેથી \( x = 30 \,\, cm\) શક્ય નથી.
આથી, વસ્તુ અંતઃર્ગોળ અરીસાની \(15 \,\, cm\) ના અંતરે હોવી જોઈએ.
અંતઃર્ગોળ અરીસા વડે રચાયેલા પ્રતિબિંબનું અંતર \( = 45 - x = 45 - 15 = 30 cm. \)
તે વાસ્તવિક , ઊલટું અને ઘણું મોટું હોય છે.
\(m\,\, = \,\,\, - \left[ {\frac{v}{u}} \right]\,\,\, = \,\,\, - \,\,\,\left[ {\frac{{ - 30}}{{ - 15}}} \right]\,\,\, = \,\,\, - 2\)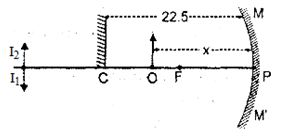
Download our appand get started for free
Similar Questions
- 1પદાર્થમાંથી નીકળતો પ્રકાશ સમતલ પ્રમાણિત અરીસા પરથી અવલોકન કાર તરફ પરાવર્તન પામે છે, તો અવલોકન કાર દ્વારા અવલોકન કરેલ પ્રતિબિંબ $.........$ હશે.View Solution
$A.$ વાસ્તવિક $B.$ ચત્તું $C.$ વસ્તુના કદ કરતા નાનું $D.$ પાર્શ્વિક વ્યત્ક્રુમિત
નીયે આપેલા વિકલ્પોમાંથી સૌથી વધુ ઉચિત ઉત્તર પસંદ કરો.
- 2$f$ કેન્દ્રલંબાઈનો અંતર્ગોળ અરીસો વસ્તુના કદ કરતા $n$ ગણું પ્રતિબિંબ રચે છે. જો પ્રતિબિંબ વાસ્તવિક હોય, તો અરીસાથી વસ્તુનું અંતર કેટલું છે ?View Solution
- 3રાતા (લાલ) પ્રકાશ માટે અને વાદળી પ્રકાશ માટે કાચનાં વક્રીભવનાંક અનુક્રમે $1.520$ અને $1.525$ છે. આ કાચનાં પ્રિઝમ માટે રાતા અને વાદળી પ્રકાશનાં લઘુત્તમ વિચલનકોણ અનુક્રમે $D_{1}$ અને $D _{2}$ હોય તોView Solution
- 4$-15\;D$ અને $5\;D$ વાળા બે લેન્સ પરસ્પર સંપર્કમાં છે. આ જોડાણની કેન્દ્રલંબાઈ કેટલી થાય?View Solution
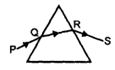
- 5View Solutionસમક્ષિતિજ ટેબલ પર મૂકેલા સમબાજુ કાચના પ્રિઝમ પર આપાત થાય છે. ન્યૂનત્તમ વિચલન માટે શું સાચું છે?
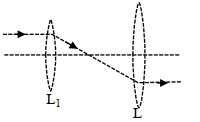
- 6નીચેની આકૃત્તિ અનુક્રમે $10 \mathrm{~cm}$ અને $15 \mathrm{~cm}$ કેન્દ્રલંબાઈ ધરાવતા બે દ્વિ-બહિર્ગોળ લેન્સ $L_1$ અને $L_2$ દર્શાવે છે. $L_1$ અને $L_2$ વચ્ચેનું અંતર ........ થશે.View Solution
- 7જ્યારે સમતલીય બહિર્ગોળ લેન્સની સમતલ સપાટી પર સિલ્વર લગાડવામાં આવે જેથી તે $ 60\, cm$ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસા તરીકે વર્તેં છે. તેમ છતાં જો બહિર્ગોળ સપાટી પર સિલ્વર લગાડવામાં આવે તો તે $20\, cm$ કેન્દ્રલંબાઈનો અંતર્ગોળ અરીસા તરીકે વર્તેં છે. તો લેન્સનો વક્રીભવનાંક શું થશે?View Solution
- 8પ્રકાશનું કિરણ અરીસાના સમતલને લંબરૂપે આપાત થાય છે.તો પરાવર્તન કોણ ......$^o$ થશે.View Solution
- 9સમતલ અરીસાથી $3\;m$ દૂર મૂકવામાં આવેલ પદાર્થના પ્રતિબિંબનો ફોટો લેવાનો છે. અરીસાથી $4.5 \;m$ અંતરે રહેલ કેમેરાને કેટલા.......$m$ અંતર માટે ફોકસ કરવું પડે?View Solution
- 10એક ફિલન્ટનાં અને બીજા ક્રાઉન કાચનાં બે પ્રિઝમોનું સંયોજન વિચલન વગર વિભાજન ઉત્પન્ન કરે છે. ફિલન્ટ કાચના પ્રિઝમનો કોણ $15^o$ છે. લાલ અને જાંબલી રંગ માટે ચોખ્ખું કોણીય નિયોજન ..... હશે. અહીં વિચલન માટે (ક્રાઉન કાચ માટે $\mu = 1.52$, ક્રાઉન કાચ માટે $\mu =1.65,$ ક્રાઉન કાચ માટે $\omega =0.20$, ફિલન્ટ કાચ માટે $\omega =0.03$).View Solution
