સીધી રેખાની સાપેક્ષે ગતિ કરતાં કણ માટે સ્થાન $(x)$ અને સમય $(t)$ વચ્ચેનો સંબંધ નીચે આપેલ છે. નીચેના સમીકરણમાંથી કયું એકરૂપ પ્રવેગીય ગતિની રજૂઆત કરે છે? [જ્યાં $\alpha$ અને $\beta$ ધન અચળાંકો છે]
Diffcult
Download our app for free and get started
d
(d)
(d)
For uniformly accelerated motion,
$v^2=u^2+2 a s$
$\quad \downarrow$
Constant
or
$s=ut+\frac{1}{2} a t^2$
$\quad \downarrow$
Constant
$x=\frac{1}{2} a t^2+u t$
Or the maximum power of $t$ has to be two.
So, $4$.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પદાર્થ $6.25\ m/s$ ની ઝડપે ગતિ કરી રહ્યો છે, તેનો પ્રતિપ્રવેગનો દર $\frac{{dv}}{{dt}} = - 2.5\sqrt v $ થી અપાય છે. જયાં, $v$ એ તત્કાલીન ઝડપ છે. પદાર્થને સ્થિર થવા માટે લાગતો સમય $(\sec$ માં$)$ કેટલો હશે?View Solution
- 2જો $v$ એ $x$ - અક્ષ સાથે ગતિ કરતાં પદાર્થનો વેગ હોય તો પદાર્થનો પ્રવેગ શું થાય?View Solution
- 3એક કણનું સ્થાનાંતર $x$ સમય $t$ સાથે $x = a{e^{ - \alpha \,t}} + b{e^{\beta \,t}}$ મુજબ બદલાય છે, જ્યાં $a ,b,\alpha$ અને $\beta$ એ ધન અચળાંક છે. કણનો વેગ ........View Solution
- 4ટાવરની ટોચથી $10 \,m / s$ ની ઝડપે બોલ ઉપરની તરફ ફેકવામાં આવે છે અને તે $20 \,m / s$ ની ઝડપ સાથે જમીન પર પહોંચે છે. ટાવરની ઉંચાઈ ............ $m$ થાય? [$g = 10 \,m / s ^2$ લો]View Solution
- 5ટાવરની ટોચ પરથી એક દડાને ઉપર તરક ફેકવામાં આવે છે જે જમીન પર $6\, s$ માં પહોંચે છે. બીજા દડાને તે જ સ્થાનેથી અધોલંબ દિશામાં નીચે તરફ સમાન ઝડપથી ફેંકવામાં આવે, તો તે $1.5 \,s$ માં જમીન પર પહોંચે છે. ત્રીજા દડાને આ જ સ્થાનેની મુક્ત પતન કરાવવામાં આવે, તો જમીન પર ......... $s$ માં પહોચશે.View Solution
- 6પ્રિતી મેટ્રો સ્ટેશન પર પહોંચીને જુએ છે, કે એસ્કેલેટર કાર્યરત નથી.તેથી તેને સ્થિર એસ્કેલેટર પર ચાલવા માટે $ t_1 $ સમય લાગે છે. બીજા દિવસે જ્યારે એસ્કેલેટર ચાલતું હોય, તો તે તેના પર ઊભા રહીને $t _{2}$ સમયમાં તે ઉપર પહોંચે છે. તે ગતિ કરતાં એસ્કેલેટર પર ચાલવા લાગે, તો તેને ઉપર પહોંચવા લાગતો સમય શું હશે?View Solution
- 7${m_1}$ અને ${m_2}$ દળના બોલને સમાન ઊંચાઈ પરથી મુક્ત કરવામાં આવે છે તો તેને જમીન પર આવતા લાગતો સમય ${t_1}$ અને ${t_2}$ હોય તોView Solution
- 8બે સમાન કારની કોઇ એક ક્ષણે ઝડપ અનુક્રમે $u$ અને $4u$ છે. તે ક્ષણથી તેઓ અમુક અંતર કાપીને સ્થિર થાય, તો બંને કારે કાપેલા અંતરનો ગુણોત્તર કેટલો થાય?View Solution
- 9View Solutionકણ માટે અંતર-સમયનો વક્ર આકૃતિમાં બતાવવામાં આવ્યો છે. કણનો મહત્તમ તત્કાલિન વેગ કયા બિંદુની આસપાસ હોય?
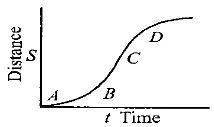
- 10એક પદાર્થનો વેગ વિરુધ્ધ સમયનો આલેખ આપેલ છે.તો તેના માટે મહત્તમ પ્રવેગ કેટલા.......$\mathrm{cm/sec}^{2}$ મળે?View Solution
