એક વિસ્તારમાં વિદ્યુતક્ષેત્ર ત્રિજ્યાકીય રીતે બહારની તરફ છે. અને કોઈ બિંદુ પાસે તે $E=250 r \,V / m$ છે ( જ્યાં $r$ એ બિંદુનો ઉદગમથી અંતર છે.). $20 \,cm$ ત્રિજ્યાના ગોળામાં ઉદગમ પાસે કેન્દ્રિત થયેલો વિદ્યુતભાર ................. $C$
Easy
Download our app for free and get started
c
(c)
(c)
\(E=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q}{r^2}\)
\(250 r=\frac{9 \times 10^9 \cdot Q}{r^2}\)
Use \(r=20 \times 10^{-2} \,m\)
Find \(Q=\) ?
\(Q=2.22 \times 10^{-10} C\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$+ q$ વિદ્યુતભાર $L$ લંબાઈના સમઘનના કેન્દ્ર પર મૂકેલો છે, તો સમઘનમાંથી કેટલું ફ્લક્સ પસાર થાય?View Solution
- 2આકૃત્તિમાં દર્શાવ્યા મુજબ, $Y$-અક્ષ પરના $P$ બિંદૂ ઓ પરિણામી વિદ્યુતક્ષેત્ર શૂન્ય હોય તો $\left|\frac{q_2}{q_3}\right|$ નો ગુણોત્તર $\frac{8}{5 \sqrt{x}}$ છે, જ્યાં $x=$. . . . . . .View Solution
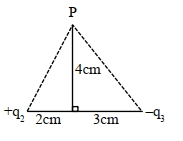
- 3બે વિદ્યુત ડાયપોલની ડાયપોલ મોમેન્ટ $P$ અને $64 \,P$ છે.આ બંને ડાયપોલને વિરુધ્ધ દિશામાં $25 \,cm$ અંતરે મૂકેલા છે.તો $P$ ડાયપોલ મોમેન્ટવાળા ડાયપોલથી કેટલા......$cm$ ના અંતરે વિદ્યુતક્ષેત્ર શૂન્ય થાય?View Solution
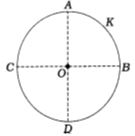
- 4એક પાતળી $R$ ત્રિજયાની સુવાહક વર્તુળાકાર રિંગ પરનો વિદ્યુતભાર $+Q$ છે. વર્તુળાકાર રિંગના $AKB$ વિભાગથી રિંગના કેન્દ્ર પર ઉદ્ભવતું વિદ્યુતક્ષેત્ર $E$ છે,તો રિંગના $ACDB $ વિભાગથી રિંગના કેન્દ્ર પર ઉદ્ભવતું વિદ્યુતક્ષેત્ર ________ હશે.View Solution
- 5$1$ થી $5$ અંકિત કરેલા પાંચ દડાઓ અલગ-અલગ દોરી વડે લટકાવેલા છે. જોડ $(2, 3)$ અને $(4, 5)$ સ્થિતવિદ્યુત અપાકર્ષણ દર્શાવે છે. જ્યારે જોડ $(1, 2),(3, 5)$ અને $(1, 5)$ સ્થિત વિદ્યુત આકર્ષણ દશાવે છે. $1$ અંકિત દડો કેવો હોવો જોઈએ?View Solution
- 6$10\, mg$ દળ ધરાવતાં બે નાના ગોળાઓને $0.5\, m$ લંબાઈની દોરી દ્વારા એક બિંદુ પરથી લટકાવવામાં આવ્યા છે. બંને પર એક સરખો વિજભાર છે અને એકબીજાને $0.20\, m$ અંતર સુધી અપાકર્ષિત કરે છે. દરેક ગોળા પરનો વિજભાર $\frac{ a }{21} \times 10^{-8} \, C$ છે તો $a$ નું મૂલ્ય ........ હશે. [$g=10 \,ms ^{-2}$ આપેલ છે. ]View Solution
- 7$R$ ત્રિજયાના ગોળા પર $2Q$ જેટલો કુલ વિદ્યુતભાર છે જેની વિદ્યુતભાર ઘનતા $\rho(r) = kr$ જ્યાં $r$ એ કેન્દ્રથી અંતર છે. બે વિદ્યુતભાર $A$અને $B$ જેનો વિદ્યુતભાર $-Q$ છે તેને ગોળાના વ્યાસ પર કેન્દ્ર થી સમાન અંતર પર છે. જો $A$ અને $B$ પર કોઈ બળ લાગતું ના હોય તો.....View Solution
- 8$a/4$ ત્રિજ્યાની તકતી જે સમાન વિતરણ વિજભાર $6 c$ ધરાવે છે. તેને $x - y$ સમતલમા $(-a / 2,0,0)$ કેન્દ્ર સાથે તે માં મૂકવામાં આવે છે.$a$ લંબાઈનો સળિયો જે સમાન વિતરણ વીજભાર $8c$ ધરાવે છે તેને $X = a / 4$ થી $X =5 a / 4$ સુધી $X - axis$ પર મૂકેલ છે. જો બિંદુવત વીજભાર $-7 c$ અને $3 c$ ને $(a / 4,-a / 4,0)$ પર અને $(-3 a / 4,3 a / 4,0)$ પર મૂકેલ છે.બે સપાટી, $x=\pm a / 2, \quad Y =\pm a / 2, \quad Z =\pm a / 2$ દ્વારા બનતા ગોળાકાર સપાટીને ધ્યાનમાં લો. તેમાંથી પસાર થતું વિદ્યુત ફ્લક્સ $..........$View Solution
- 9ડાઈપોલ માટે $q = 2 × 10^{-6}\ C ; d = 0.01\ m$ જો $E = 5 ×10^{5}\ N/C $ હોય તો ડાઈપોલ પર લાગતું મહત્તમ ટોર્ક શોધો.View Solution
- 10બે બિંદુવત વિધુતભારો $+q$ અને $-q$ ને $(-d, 0)$ અને $(d, 0)$ પર $x -y$ સમતલમાં મૂકેલા હોય તોView Solution