એક વર્તુળાકાર તકતી $L$ લંબાઈના ઢાળ પરથી ઉપરથી નીચે આવે છે, જ્યારે તે ઢાળ પર સરકીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{1}$ છે. જ્યારે તે ગબડીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{2}$ છે. તો $\frac{t_{2}}{t_{1}}$ નું મૂલ્ય $\sqrt{\frac{3}{x}}$ છે, તો $x$ નું મૂલ્ય કેટલું હશે?
JEE MAIN 2021, Diffcult
d
If disk slips on inclined plane, then it's aceleration
If disk slips on inclined plane, then it's aceleration
\(a_{1}=g \sin \theta\)
\(L=\frac{1}{2} a_{1} t_{1}^{2}\)
\(\Rightarrow t_{1}=\sqrt{\frac{2 L}{a_{1}}}\ldots \ldots({i} )\)
If disk rols on inclined plane, its acceleration,
\(a_{2} =\frac{g \sin \theta}{1+\frac{I}{m R^{2}}}\)
\(a_{2} =\frac{g \sin \theta}{1+\frac{m R^{2}}{2 m R^{2}}}\)
\(a_{2} =\frac{2}{3} g \sin \theta\)
Now \({L}=\frac{1}{2} {a}_{2} \cdot {t}_{2}^{2}\)
\(\Rightarrow {t}_{2}=\sqrt{\frac{2 {L}}{{a}_{2}}} \quad \ldots \ldots({ii} )\)
Now \(\frac{t_{2}}{t_{1}}=\sqrt{\frac{a_{1}}{a_{2}}}=\sqrt{\frac{3}{2}}\)
\(\Rightarrow {x}=2\)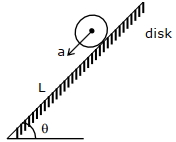
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$50\,cm$ લાંબી એક નળીમાં $250\,g$ દળ ધરાવતું અદબનીય પ્રવાહી ભરેલું છે અને તે બંને છેડાઓથી બંધ કરેલ છે. ત્યારબાદ નળીને તેના એક છેડાને ફરતે સમક્ષિતિજ સમતલમાં $x \sqrt{F} \;rad s ^{-1}$ જેટલા નિયમિત કોણીયવેગથી ભ્રમણ કરાવવામાં આવે છે. જો $F$ એ પ્રવાહી દ્વારા બીજા છેડા પર લાગતું બળ હોય તો $x$ નું મૂલ્ય થશે.View Solution
- 2અચળ કદ $V$ ધરાવતા ગોળા ની જડત્વની ચાકમાત્રા $I$ હોય તો $I$ અને $V$ વચ્ચેનો સંબંધ ?View Solution
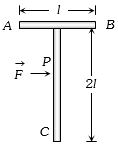
- 3આકૃતિમાં દર્શાવ્યા મુજબ $ T $ આકારનો પદાર્થ લીસી સપાટી પર છે. હવે બિંદુ $ P $ પર,$ AB $ ને સમાંતર દિશામાં બળ $\mathop F\limits^ \to $ એવી રીતે લગાવવામાં આવે છે, જેથી પદાર્થ ચાકગતિ કર્યા વિના ફક્ત રેખીય ગતિ કરે, તો બિંદુ $ C$ ની સાપેક્ષે બિંદુ $P$ નું સ્થાન શોધો.View Solution
- 4જેની દળ ધનતા $\rho{=\rho_0}\left(1-\frac{x^2}{L^2}\right) kg / m$ અને લંબાઈ $L$ (મીટરમાં) હોય તેવા એક પરિમાણીય સળિયાનું, એક છેડાથી દ્રવ્યમાન કેન્દ્ર $\frac{3 L}{\alpha}$ મીટર છે. $\alpha$ નું મૂલ્ય $........$ હશે.View Solution
- 5$R$ ત્રિજ્યાની એક નિયમિત વર્તુળાકાર તકતીમાથી એક ચતુર્થ ભાગ કાપી લેવામાં આવે છે. તે ભાગનું દળ $M$ છે. મૂળ તકતીના કેન્દ્રમાથી પસાર થતી અને કાપેલા ભાગના સમતલને લંબ અક્ષ ને અનુલક્ષીને તે ભાગ ભ્રમણ કરે છે. તો તેની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા શું હશે?View Solution
- 6કોઇ બિંદુ $\overrightarrow {R} = 2\hat i - 6\hat j - 12\hat k$ પર એક બળ $\overrightarrow {F} = \alpha \hat i + 3\hat j + 6\hat k$ લાગે છે. $\alpha $ ના કયા મૂલ્ય માટે ઊગમબિંદુને અનુલક્ષીને કોણીય વેગમાનનું સંરક્ષણ થશે?View Solution
- 7$L$ લંબાઈ અને $M$ દળ ધરાવતો એક પાતળો સળિયો તેને લંબ અને તેના કેન્દ્રમાથી પસર થતી અક્ષને અનુલક્ષીને ${\omega _0}$ ના અચળ કોણીય ઝડપથી ભ્રમણ કરે છે.બે $m$ દળ અને નહિવત પરિમાણ ધરાવતા મણકા શરૂઆતમાં સળિયાના કેન્દ્ર પર છે,જે સળિયા પર મુક્ત રીતે ભ્રમણ કરી શકે છે. જ્યારે મણકા સળિયાના છેડા પર હોય ત્યારે તંત્રની કોણીય ઝડપ કેટલી થશે?View Solution
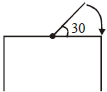
- 8$1\; \mathrm{m}$ લાંબા સળિયાનો એક છેડો સમક્ષિતિજ ટેબલ પર જડેલો છે.જ્યારે તે સમક્ષિતિજ સાથે $30^{\circ}$ નો ખૂણો બનાવે ત્યારે તેણે મુક્ત કરવામાં આવે છે.તે જ્યારે ટેબલ સાથે અથડાય ત્યારે તેનો કોણીય વેગ $\sqrt{\mathrm{n}}\; \mathrm{s}^{-1}$ આપવામાં આવે છે જ્યાં $\mathrm{n}$ એ પૂર્ણાંક સંખ્યા હોય તો $n$ મૂલ્ય કેટલું હશે?View Solution
- 9એક વ્હીલએ તેની સમાંતર અક્ષને અનુલક્ષીને $4 \,kg m ^2$ ની જડત્વની ચાક્રમાત્રા ધરાવે છે. તે અક્ષનો અનુલક્ષીને $240 \,rpm$ ની ઝડપે ભ્રમણ કરે છે. તો એક મિનિટ માં વ્હીલનું પરિભ્રમણ અટકાવવા માટે ........... $Nm$ ટોર્કની જરુર પડે?View Solution
- 10આકૃતિમાં ચિત્ર તરફ જુઓ કે જે સમાન રેખીય જડાઈની શાહી થી દોરેલ છે. બે આંતરીક વર્તૂળો દોરવા માટે અને બે રેખાઓના વૃત્તખંડ દોરવા માટે શાહીના $m $ દળનો ઉપયોગ થાય છે $6\ m$ જેટલું બહારની વર્તૂળ દોરવા માટે શાહીના દળનો ઉપયોગ કરેલ છે. જુદા જુદા ભાગોના કેન્દ્રોના યામાક્ષો બહારના વર્તૂળ $(0, 0)$ ડાબી તરફના આંતરિક વર્તૂળ $ (a, a)$ અને સમક્ષિતિજ રેખા $ (0, a)$ છે. ચિત્રમાં શાહીના દ્રવ્યમાન કેન્દ્રનો $y$ યામાક્ષ શોધો.View Solution