આકૃતિમાં દર્શાવ્યા મુજબ $ T $ આકારનો પદાર્થ લીસી સપાટી પર છે. હવે બિંદુ $ P $ પર,$ AB $ ને સમાંતર દિશામાં બળ $\mathop F\limits^ \to $ એવી રીતે લગાવવામાં આવે છે, જેથી પદાર્થ ચાકગતિ કર્યા વિના ફક્ત રેખીય ગતિ કરે, તો બિંદુ $ C$ ની સાપેક્ષે બિંદુ $P$ નું સ્થાન શોધો.
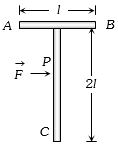
AIEEE 2005, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$m_1$ અને $ m_2$ દળના બે કણોના તંત્રના દ્રવ્યમાન કેન્દ્રનું સ્થાન સદિશ શોધો. તેઓ એકબીજાથી $ L$ અંતરે રહેલાં છે.View Solution
- 2એક સ્થિર સ્થિતિમાં રહેલું પૈડું અચળ કોણીય પ્રવેગ થી ફરવાનું સારું કરે છે જો તે પ્રથમ $1\ sec$ માં $\theta_1 $ અને બીજી સેકંડ માં $\theta_2 $ કોણીય અંતર કાપે તો $\theta_2 \over \theta_1 $ =View Solution
- 3એક કણ સ્થિર સ્થિતિમાથી $\theta = 0.025{t^2} - 0.1t$ મુજબ ગતિ કરવાનું ચાલૂ કરે છે જ્યાં $\theta $ radian માં અને $t \,seconds$ માં છે તો કણ નો કોણીય પ્રવેગ કેટલો થાય $?$View Solution
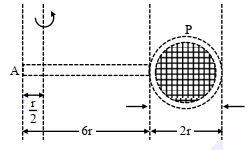
- 4આકૃતિમાં એક બેડમિન્ટન રેકેટના પરિમાણ આપેલા છે. જો બેડમિન્ટનના રેખીય અને વર્તુળાકાર ભાગનું સમાન દળ $(M)$ અને દોરીનું દળ અવગણ્ય હોય તો, હેન્ડલના બિંદુ $A$ થી $\frac{r}{2}$ અંતરે રેકેટના હેન્ડલને લંબ અને રિંગના સમતલમાં રહેલી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા ....... $Mr^2$ જેટલી થાય?View Solution
- 5સમક્ષિતિજ સાથે કોણ ધરાવતા ઢાળ પરથી $R$ ત્રિજ્યાવાળો, $M$ દળ ધરાવતો પદાર્થ સરક્યા વિના ગબડે છે. જો પદાર્થની જડત્વની ચાકમાત્રા $ I $ હોય, તો પદાર્થનો પ્રવેગ .......View Solution
- 6View Solutionસૌરમંડળમાં ગ્રહોની ગતિ એ ...... સંરક્ષણનું ઉદાહરણ છે.
- 7એક વર્તુળાકાર તકતી $L$ લંબાઈના ઢાળ પરથી ઉપરથી નીચે આવે છે, જ્યારે તે ઢાળ પર સરકીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{1}$ છે. જ્યારે તે ગબડીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{2}$ છે. તો $\frac{t_{2}}{t_{1}}$ નું મૂલ્ય $\sqrt{\frac{3}{x}}$ છે, તો $x$ નું મૂલ્ય કેટલું હશે?View Solution
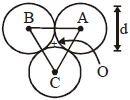
- 8$\mathrm{m}$ દળ અને $d$ વ્યાસ ધરાવતા ત્રણ ઘન ગોળા એવી રીતે જોડાયેલા છે કે જેથી તેમના કેન્દ્રને જોડતા તે $d$ લંબાઇનો સમબાજુ ત્રિકોણ બનાવે.જો $\mathrm{I}_{0}$ એ તેમના દ્રવ્યમાન કેન્દ્ર અને $\mathrm{I}_{\mathrm{A}}$ એ કોઇ એક ગોળાના કેન્દ્રમાથી અને ત્રિકોણના સમતલને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા હોય તો $\mathrm{I}_{0} / \mathrm{I}_{\mathrm{A}}$ નો ગુણોત્તર કેટલો મળે?View Solution
- 9પાતળી ધાતુની તકતીમાંથી $ R$ ત્રિજ્યાનું વર્તૂળાકાર કાપી નાંખેલ છે. $R/2$ ત્રિજ્યાનું છિદ્ર આ વર્તૂળમાંથી કરવામાં આવે છે. આ રીતે વર્તૂળની રીમને સ્પર્શેં છે. તેનું મૂળ કાપ્યા વગરના ભાગના દ્રવ્યમાન કેન્દ્રથી અંતર શોધો.View Solution
- 10સમાન દળ અને જુદી-જુદી ત્રિજ્યાઓ ધરાવતી બે તક્તિઓ કે જે જુદા-જુદા દ્રવ્યોની બનેલી છે તે એવી રીતે બનાવવામાં આવે છે કે જેથી તેની જાડાઈ અનુક્રમે $1\,cm$ અને $0.5\,cm$ હોય. દ્રવ્યની ઘનતાઓ $3:5$ ના ગુણોતરમાં છે. આ તક્તિઓની તેમનાં વ્યાસને અનુલક્ષીને જડત્વની ચાક્માત્રાઓ $\frac{x}{6}$ નાં ગુણોતરમાં મળે છે. $x$ નું મૂલ્ય $........$ થશે.View Solution