એલ્યુમિનિયમ અને કોપર જેવા દ્રવ્યો માટે સ્થિતિસ્થાપક અંકનો સાચો ક્રમ નીચેનામાથી કયો છે?
JEE MAIN 2014, Medium
c
Poisson's ratio,
Poisson's ratio,
\(\sigma = \frac{{Iateral\,strain\left( \beta \right)}}{{longitudinal\,strain\left( \alpha \right)}}\)
For material like copper, \(\sigma = 0.33\)
\(And,\,y = 3k\left( {1 - 2\sigma } \right)\)
\(Also,\frac{9}{y} = \frac{1}{k} + \frac{3}{n}\)
\(y = 2n\left( {1 + \sigma } \right)\)
\(Hence,n < y < k\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન દ્રવ્યના બે તારની લંબાઇનો ગુણોત્તર $1 : 2$ અને વ્યાસનો ગુણોત્તર $2 : 1$ છે.તેના પર $F_A$ અને $F_B$ બળ લાગતાં લંબાઇમાં સમાન વધારો થાય છે,તો $\frac{F_A}{F_B} =$View Solution
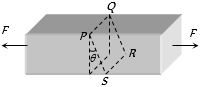
- 2$PQRS$ આડછેદ પર તણાવ પ્રતિબળ મહત્તમ થવા માટે $\theta =$ ......... $^o$View Solution
- 3બે તાર $A$ અને $B$ ને સમાન બળથી ખેંચવામા આવે છે જો $A$ અને $B$ માટે $Y_A: Y_B=1: 2, r_A: r_B=3: 1$ અને $L_A: L_B=4: 1$ તો $\left(\frac{\Delta L_A}{\Delta L_B}\right)$ કેટલું હશે.View Solution
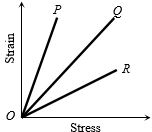
- 4નીચે ત્રણ તાર $P, Q$ અને $R$ માટે વિકૃતિ વિરુદ્ધ પ્રતિબળ નો ગ્રાફ આપેલો છે તો ગ્રાફ પરથી નીચેનામાથી શું સાચું છે $?$View Solution
- 5View Solutionકયો સ્થિતિસ્થાપકતા અંક પ્રવાહી માટે વપરાય છે.
- 6$K$ બળ અચળાંક ધરાવતી સ્પ્રિંગની લંબાઈ $l_1$ થી $l_2$ કરવા કેટલું કાર્ય કરવું પડે$?$View Solution
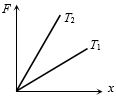
- 7નીચેના ગ્રાફમાં એક પાતળા તાર માટે બે તાપમાન $T_1$ અને $T_2$ માટે પ્રતિબળ વિરુદ્ધ લંબાઈમાં થતો ફેરફાર દર્શાવેલ છે તો તે શું દર્શાવે છે $?$View Solution
- 8$20\; kg$ દળ, $0.4\; m ^2$ નું આડછેદ અને $20\,m$ લંબાઈના એક નિયમિત ભારે સળિયાને જડિત આધાર પરથી લટકાવવામાં આવે છે. ક્ષેત્રીય $(lateral)$ સંકોચન અવગણતા, સળિયામાં વિસ્તરણ $x \times 10^{-9}\; m$ મળે છે. $x$ નું મૂલ્ય $...........$ હશે. ($Y =2 \times 10^{11} \;Nm ^{-2}$ and $\left.g=10\, ms ^{-2}\right)$View Solution
- 9યંગ મોડયુલસ $Y,$ બલ્ક મોડયુલસ $K$ અને આકાર સ્થિતિસ્થાપકતા અંક $\eta $ વચ્ચેનો સંબંધ $?$View Solution
- 10View Solutionતાપમાનના વધારા સાથે સ્થિતિસ્થાપકતતાનો યંગ ગુણાંક
