$20\; kg$ દળ, $0.4\; m ^2$ નું આડછેદ અને $20\,m$ લંબાઈના એક નિયમિત ભારે સળિયાને જડિત આધાર પરથી લટકાવવામાં આવે છે. ક્ષેત્રીય $(lateral)$ સંકોચન અવગણતા, સળિયામાં વિસ્તરણ $x \times 10^{-9}\; m$ મળે છે. $x$ નું મૂલ્ય $...........$ હશે. ($Y =2 \times 10^{11} \;Nm ^{-2}$ and $\left.g=10\, ms ^{-2}\right)$
JEE MAIN 2022, Diffcult
b
\(Y =\frac{ T }{ A } \frac{ dx }{ dy }\)
\(Y =\frac{ T }{ A } \frac{ dx }{ dy }\)
\(m =20\,kg\)
\(A =0.4\,m^{2}\)
\(1=20\,m\)
let extension is \(dy\) in length \(dx\)
\(Y =\frac{\text { stress }}{\text { strain }}\)
\(Y =\frac{\frac{ T }{ A }}{\frac{ d }{ dx }}=\frac{ T }{ A } \cdot \frac{ dx }{ dy }\)
\(dy =\frac{ Tdx }{ AY }\)
Tension at a distance \(x\) from lower end \(=\frac{ mg }{\ell} x\)
So. \(\int_{0}^{\Delta l} dy =\int_{0}^{\ell} \frac{ mg }{\ell} x \frac{ dx }{ AY }\)
\(\Delta \ell=\frac{ mg }{\ell AY }\left[\frac{ x ^{2}}{2}\right]_{0}^{\ell}\)
\(\Delta \ell=\frac{ mg \ell}{2\,AY }\)
\(\Delta \ell=\frac{20 \times 10 \times 20}{2 \times 0.4 \times 2 \times 10^{11}}\)
\(2500 \times 10^{-11}\)
\(\Delta \ell=25 \times 10^{-9}\)
\(= x \times 10^{-9}\)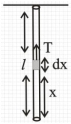
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમઘનની નીચેની બાજુ આધાર સાથે દઢ કરેલી છે. એની ઉપરની બાજુએ $30°$ ના ખૂણે બળ લગાવવામાં આવે તો તેમાં શેમાં ફેરફાર થાય ?View Solution
- 2રબરનો યંગ મોડ્યુલસ ${10^4}\,N/{m^2}$ અને આડછેદનું ક્ષેત્રફળ $2\,c{m^2}$ છે.જો તેની લંબાઇની દિશામાં $2 \times {10^5}$ dynes બળ લગાવવામાં આવે તો તેની લંબાઈ કેટલી થાય ?View Solution
- 3$l$ લંબાઈ અને $m$ દળ ધરાવતો સળીયો ઉભી રેખામાં $M$ દળના પદાર્થ સાથે લટકેલ છે. તો તણાવ પ્રતીબળ અંતર $x$ તેના મુખ્ય ટેકાથી.... ($A \rightarrow$ સળીયાના આડછેદનું ક્ષેત્રફળ)View Solution
- 4બે તારો સમાન દ્રવ્યના બનેલા છે અને સરખું કદ ધરાવે છે. પહેલા તારના આડછેદનું ક્ષેત્રફળ $ A$ અને બીજા તારના આડછેદનું ક્ષેત્રફળ $3A$ છે. જો $F$ જેટલું બળ આપીને પહેલા તારની લંબાઇમાં $\Delta l$ નો વધારો કરવામાં આવે છે, બીજા તારની લંબાઇમાં સમાન વધારો કરવા માટે કેટલું બળ લગાવવું જોઈએ?View Solution
- 5View Solutionતાપમાનના વધારા સાથે સ્થિતિસ્થાપકતતાનો યંગ ગુણાંક
- 6તારની લંબાઈ $50\, cm$ અને આડછેદનું ક્ષેત્રફળ $1\,m{m^2}$ છે તારનો યંગ મોડ્યુલસ $2 \times {10^{10}}\,N/{m^2}$ છે.તારની લંબાઈમાં $1 \,cm$ નો વધારો કરવા માટે જરૂરી કાર્ય કેટલું હોવું જોઈએ $?$View Solution
- 7કોલમ $-I$માં આપેલી માહિતી પરથી કોલમ $-II$ સાથે યોગ્ય રીતે જોડો :View Solution
કોલમ $-I$ કોલમ $-II$ $(a)$ પ્રતિબળ એ વિકૃતિના સમપ્રમાણમાં હોય
$(i)$ સ્થિતિસ્થાપક હદ $(b)$ તાર પરનો બોજ દૂર કરતાં તે પોતાના મૂળ પરિમાણમાં પાછો ફરે છે. $(ii)$ સમપ્રમાણની હદ $(iii)$ પ્લાસ્ટિક વિરૂપણ - 8એક છડેથી જડિત કરેલા સ્ટીલના તાર $A$ પર બળ લગાડવામાં આવે છે. પરિણામે તેની લંબાઈમાં $0.2\,mm$ નો વધારો ઉદભવે છે. તાર $A$ કરતા બમણી લંબાઈ અને $2.4$ ગણો વ્યાસ ધરાવતા બીજા સ્ટીલ તાર $B$ ને આટલું જ બળ લગાડવામાં આવે તો તાર $B$ ની લંબાઇમાં થતો વધારો $..........\times 10^{-2}\,mm$ થાય.(બંને તાર સમાન વર્તુળાકાર આડછેદ ધરાવે છે.)View Solution
- 9$L$ મીટર લંબાઈ અને $A$ મીટર$^2$ આડછેદનું ક્ષેત્રફળ ધરાવતા તારને છત સાથે બાંધેલો છે. જેની ઘનતા $D$ $kg/metr{e^3}$ અને યંગ મોડ્યુલસ $E$ $newton/metr{e^2}$.જો તારની લંબાઈ પોતાના વજનને લીધે $l$ જેટલી વધતી હોય તો $l=$____View Solution
- 10માધ્યમનું દબાણ $1.01 × 10^5$ $Pa$ થી $1.165 × 10^5$ $Pa$ અને તાપમાન અચળ રાખીને કદમાં થતો ફેરફાર $10\ %$ હોય તો માધ્યમનો બલ્ક મોડ્યુલસ કેટલો હશે $?$View Solution
