સમાન દ્રવ્યના બે તારની લંબાઇનો ગુણોત્તર $1 : 2$ અને વ્યાસનો ગુણોત્તર $2 : 1$ છે.તેના પર $F_A$ અને $F_B$ બળ લાગતાં લંબાઇમાં સમાન વધારો થાય છે,તો $\frac{F_A}{F_B} =$
Medium
Download our app for free and get started
d
\(Y = \frac{{FL}}{{\pi {r^2}l}}\)
\(Y = \frac{{FL}}{{\pi {r^2}l}}\)
\(\therefore \,\,F = Y\pi {r^2}\frac{l}{L}\)
\(\frac{{{F_A}}}{{{F_B}}} = \frac{{{Y_A}}}{{{Y_B}}}{\left( {\frac{{{r_A}}}{{{r_B}}}} \right)^2}\left( {\frac{{{l_A}}}{{{l_B}}}} \right)\,\left( {\frac{{{L_B}}}{{{L_A}}}} \right)\)
\( = 1 \times {\left( {\frac{2}{1}} \right)^2} \times \left( 1 \right) \times \left( {\frac{2}{1}} \right) = 8\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionએક બીમ બે છેડે ટેકવેલો છે,તો કેન્દ્ર પાસે વંકન કોના સપ્રમાણમાં હોય?
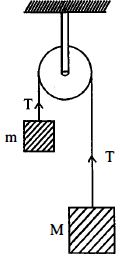
- 2બે $m$ અને $M$ દળ ધરાવતા બ્લોકને $A$ આડછેડનું ક્ષેત્રફળ ધરાવતા તાર સાથે જોડે ઘર્ષણરહિત ગરગડી પર આકૃતિમાં દર્શાવેલ મુજબ મૂકેલા છે.હવે તંત્રને મુક્ત કરવામાં આવે છે જો $M = 2 m$ હોય તો તારમાં ઉત્પન્ન થતું પ્રતિબળ કેટલું હશે?View Solution
- 3View Solutionસંપૂર્ણ કઠોર પદાર્થ માટે યંગ મોડયુલસનું મૂલ્ય ............... છે.
- 4સમઘનની નીચેની બાજુ આધાર સાથે દઢ કરેલી છે. એની ઉપરની બાજુએ $30°$ ના ખૂણે બળ લગાવવામાં આવે તો તેમાં શેમાં ફેરફાર થાય ?View Solution
- 5ઉપરના છેડે જડિત કરેળ તાર પર $F$ બળ લગાવીને લંબાઈ $l$ સુધી લંબાય છે. તો તારાને ખેંચવા માટે કેટલું કાર્ય કરવું પડે?View Solution
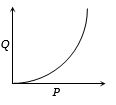
- 6હુકના નિયમનું પાલન થાય ત્યાં સુધીના ગાળા માટે તાર માટે એક ગ્રાફ દર્શાવેલ છે તો આ ગ્રાફ માં $P$ અને $Q$ શું હશે $?$View Solution
- 7યંગ મોડ્યુલસ શોધવાના પ્રયોગમાં $5\, mm$ ત્રિજ્યા અને $1 \,m$ લંબાઈ ધરાવતા પાતળા તારના એક છેડા પર $50\,\pi kN$ નું બળ લગાવવામાં આવે છે. બધી લંબાઈના માપનમાં લેવાતા સાધનની લઘુતમ માપશક્તિ $0.01\, mm$ હોય તો નીચે પૈકી કયું વિધાન ખોટું પડે?View Solution
- 8તારનો એક છેડો છત સાથે જડિત છે અને બીજા છેડાથી $2 \mathrm{~kg}$ નું દળ લટકાવેલ છે. આવો સમાન બીજો તાર ભારના છેડે થી લટકાવવામાં આવે છે અને નીચેના તારને છેડે $1 \mathrm{~kg}$ નું દળ લટકાવવામાં આવે છે. તો ઉપરના તારમાં અને નીચેના તારમાં પ્રવર્તતી સંગતવિકૃતિતોનો ગુણોત્તર_____________હશે.View Solution
[તારનો આડઇેદનું ક્ષેત્રણ $=0.005 \mathrm{~cm}^2 \gamma=2 \times 10^{11} \mathrm{Nm}^{-2}$ અને $\mathrm{g}=10 \mathrm{~ms}^{-2}$ ]
- 9ચોકકસ કદ $V$ નો તાંબાનો $ l $ લંબાઇનો તાર બનાવ્યો છે. આ તાર પર અચળ બળ $F$ લગાડવાથી તેની લંબાઇમાં $ \Delta l$ જેટલો વધારો થાય છે. નીચે આપેલા સંબંધમાંથી કોનો આલેખ સીધી રેખા મળે?View Solution
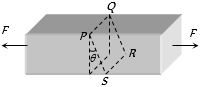
- 10$PQRS$ આડછેદ પર સ્પર્શીય પ્રતિબળ મહત્તમ થવા માટે $\theta =$ ....... $^o$View Solution
