એસિડ દ્રાવણમાં થતા એસિટોનના બ્રોમીનેશનને નીચેના સમીકરણ વડે દર્શાવાય છે.
$CH_3COCH_{3(aq)} + Br_{2(aq)} \rightarrow $$CH_3COCH_2Br_{(aq)} + H^+_{(aq)}+ Br^-_{(aq)}$
નીચેની પ્રક્રિયા સાંદ્રતા પરથી આ ગતિકીય માહિતી મળે છે.
શરૂઆતની સાંદ્રતા, $M$
| $[CH_3COCH_3]$ | $[Br_2]$ | $[H^+]$ |
| $0.30$ | $0.05$ | $0.05$ |
| $0.30$ | $0.10$ | $0.05$ |
| $0.30$ | $0.10$ | $0.10$ |
| $0.40$ | $0.05$ | $0.20$ |
$Br_2$ ના દૂર થવાનો શરૂઆતનો દર $Ms^{-1}$ માં નીચે મુજબ છે.
$5.7 \times 10^{-5} ,$ $5.7 \times 10^{-5} ,$ $1.2 \times 10^{-5} ,$ $3.1 \times 10^{-5}$
આ માહિતીને આધારે વેગ સમીકરણ ...... થશે.
AIPMT 2008, Advanced
Download our app for free and get started
c
By comparing the rate and concentration, the order of the reaction can be calculated. Let the rate of the reaction wrt \(\left[\mathrm{CH}_{3} \mathrm{COCH}_{3}\right],\left[\mathrm{Br}_{2}\right]\) and \(\left[\mathrm{H}^{+}\right]\) are \(\mathrm{x}, \mathrm{y}\) and \(z\) respectively.
By comparing the rate and concentration, the order of the reaction can be calculated. Let the rate of the reaction wrt \(\left[\mathrm{CH}_{3} \mathrm{COCH}_{3}\right],\left[\mathrm{Br}_{2}\right]\) and \(\left[\mathrm{H}^{+}\right]\) are \(\mathrm{x}, \mathrm{y}\) and \(z\) respectively.
Thus,
Rate \(\propto\left[\mathrm{CH}_{3} \mathrm{COOH}_{3}\right]^{\mathrm{X}}\left[\mathrm{Br}_{2}\right]^{\mathrm{Y}}\left[\mathrm{H}^{+}\right]^{z}\)
\(5.7 \times 10^{-5}=[0.30]^{x}[0.05]^{y}[0.05]^{z}\) ..... \((i)\)
\(5.7 \times 10^{-5}=[0.30]^{\times}(0.10)^{y}(0.05)^{z}\) ..... \((ii)\)
\(1.2 \times 10^{4}=[0.30)^{x}(0.10)^{y}(0.10)^{z}\) ..... \((iii)\)
\(3.1 \times 10^{-4}=[0.40]^{x}(0.05)^{y}(0.20)^{z} \) ..... \((iv)\)
From eqs \((i)\) and \((ii)\)
\(\mathrm{v}=0\)
From eqs \((ii)\) and \((iii)\)
\(z=1\)
From eqs \((i)\) and \((iv)\)
\(x=1\)
Thus, rate law \(\propto\left[\mathrm{CH}_{3} \mathrm{COCH}_{3}\right]\left[\mathrm{H}^{+}\right]\)
\(=\mathrm{k}\left[\mathrm{CH}_{3} \mathrm{COCH}_{3}\right]\left[\mathrm{H}^{+}\right]\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1${A} \rightarrow {B}$ પ્રક્રિયા માટે, દર અચળાંક ${k}$ એ ${s}^{-1}$માં $\log _{10} {k}=20.35-\frac{\left(2.47 \times 10^{3}\right)}{{T}}$ દ્વારા આપવામાં આવે છે. સક્રિયકરણની ઊર્જા $.....$ ${kJ} \,{mol}^{-1}$ છે. (નજીકના પૂર્ણાંકમાં) $\left[\right.$ આપેલ છે $\left.: {R}=8.314\, {~J}\, {~K}^{-1}\, {~mol}^{-1}\right]$View Solution
- 2View Solutionપ્રક્રિયા દરની સંઘાત પદ્ધતિના આધારે.....
- 3આર્હેંનિયસ સમીકરણમાં પ્રક્રિયાનાં દરને $k\, = \,\,A{e^{ - {E_a}/RT}}$તરીકે સમજાવાય. જ્યાં $E_a$ શું દર્શાવે છે?View Solution
- 4પ્રથમ ઓર્ડર પ્રક્રિયા માટે $A \rightarrow 2 B$માં $100$ મિનિટ પછી $1$ મોલ પ્રક્રિયક $A$ પછી $B$ ના $0.2$ મોલ્સ આપે છે. પ્રક્રિયાનું અર્ધઆયુષ્ય $.....\,min$ છે. [ઉપયોગ કરો $: \ln 2=0.69, \ln 10=2.3$View Solution
$log$નો ગુણધર્મ $\ln \left(\frac{{x}}{{y}}\right)=\ln {x}-\ln {y}$
- 5નીચેના આંકડા મુજબ, પ્રક્રિયાના એન્થાલ્પી ફેરફારની તીવ્રતાView Solution
${A}+{B} \rightarrow {M}+{N}$ $......$ ${kJ} {mol}^{-1}$ બરાબર છે. (નજીકના પૂર્ણાંકમાં)
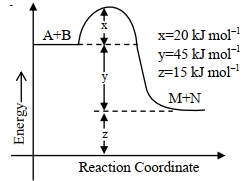
- 6$_{92}U^{235}$ નો ક્ષય.......... ક્રમની પ્રક્રિયા છે.View Solution
- 7એક પ્રક્રિયા $2A+ B \rightarrow$ નીપજ, ની ગતિકી અભ્યાસ દરમ્યાન નીચેના પરિણામો મળ્યા :View Solution
પ્રયોગ $[A]$
($mol\, L^{-1})$
$[B]$
($mol\, L^{-1})$
પ્રક્રિયાની શરૂઆતનો દર
$(mol\, L^{-1}$ $min^{-1})$
$I$ $0.10$ $0.20$ $6.93 \times {10^{ - 3}}$ $II$ $0.10$ $0.25$ $6.93 \times {10^{ - 3}}$ $III$ $0.20$ $0.30$ $1.386 \times {10^{ - 2}}$ $A$ અડધો વપરાય તે માટેનો સમય મિનિટમાં કેટલો થાય
- 8પ્રક્રિયા $2N_2O_5\,(g) \to 4NO_2\,(g) + O_2\,(g)$ એ પ્રથમ ક્રમની ગતિકીને અનુસરે છે. ફ્ક્ત $N_2O_5$ ધરાવતા પાત્રના દબાણમાં $30$ $min$ એ $50$ $mm$ $Hg$ થી વધીને $87.5$ $mm$ $Hg$ થાય છે. તો $60$ $min$ બાદ વાયુઓ દ્વારા દર્શાવાતુ દબાણ કેટલુ થશે ? (તાપમાન અચળ રહે છે તેમ ધારો)View Solution
- 9$H_2O_2$ ના વિઘટનની પ્રક્રિયાનો વેગ અચળાંક $3.66 \times 10^{-3}\,s^{-1}$ છે. જો $H_2O_2$ ની શરૂઆતની સાંદ્રતા $0.882\, M$ હોય, તો ........ $\sec$ એ તેની સાંદ્રતા $0.600\,M$ થશે.View Solution
- 10$87.5 \%$ પ્રક્રિયા પૂર્ણ થવા માટે જરૂરી સમય $t_{87.5}$ છે અને $50 \%$ પ્રક્રિયા પૂર્ણ થવા માટે જરૂરી સમય $t _{50}$ છે. $t _{87.5}=x \times t _{50}$ સંબંધ ધરાવે છે.તો $x$ નું મૂલ્ય $........$ છે.View Solution