For collision of a nenutron with deuterium \(:\)
Applying conservation of momentum\(:\)
\(m v+0=m v_{1}+2 m v_{2} \dots(i)\)
\(v_{2}-v_{1}=v \ldots(ii)\)
Therefore, Collision is elastic, \(e=1\)
From equ \((i)\) and equ \((ii)\) \(v_{1}=-v / 3\)
\(P_{d}=\frac{\frac{1}{2} m v^{2}-\frac{1}{2} m v_{1}^{2}}{\frac{1}{2} m v^{2}}=\frac{8}{9}=0.89\)
Now, for the collision of neutron with carbon nucleus
Applying conservation of momentum
\(m v+0=m v_{1}+12 m v_{2} \ldots\) \((iii)\)
\(v=v_{2}-v_{1}\) \(...(iv)\)
\(v_{1}=-\frac{11}{13} v\)
\(P_{0}=\frac{\frac{1}{2} m v^{2}-\frac{1}{2} m\left(\frac{11}{13} v\right)^{2}}{\frac{1}{2} m v^{2}}=\frac{48}{169} \approx 0.28\)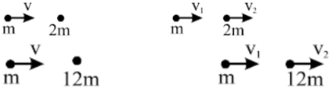
Download our appand get started for free
Similar Questions
- 1$100 m$ ઉંડાઈ પર આવેલ પંપમાંથી પ્રતિ કલાકે $7200 kg$ પાણી લઈ શકાય છે પંપનો પાવર ....... $kW$ છે. ધારો કે તેની ક્ષમતા $50\%$ છે.View Solution
- 2નીચેના બે વિધાનો પરથી આપેલ વિકલ્પમાંનો જવાબ શોધો. વિધાન $-1$ : એક જ દિશામાં ગતિ કરતા બે કણો સંપૂર્ણ અસ્થિતિસ્થાપક સંઘાતમાં તેમની બધી જ ઊર્જા ગુમાવતા નથી.View Solution
વિધાન $-2$ : બધા જ પ્રકારના સંઘાતો માટે રેખીય વેગમાન સંરક્ષણનો નિયમ પળાય છે.
- 3$m $ દળનો એક પથ્થર $20 cm$ ત્રિજ્યાવાળા શિરોલંબ વર્તૂળમાં ભ્રમણ કરે છે. ન્યુનત્તમ અને મહત્તમ સ્થાન વચ્ચેનો ગતિઊર્જાનો તફાવત કેટલો હશે ?View Solution
- 4$m$ દળ એક બ્લોક ને $\frac{g}{3}$ અચળ પ્રવેગે શિરોલંબ રીતે ઉપર તરફ $h$ અંતર જેટલું ખેંચવા માટે એક દોરીના ઉપયોગ કરવામાં આવે છે. દોરીમાંના તણાવ વડે થયેલ કાર્ય છે...View Solution
- 5વિધાન $-1$ અને વિધાન $-2$ આવેલા છે. જો $S_1$ અને $S_2$ બે સ્પ્રિંગના બળ અચળાંકો અનુક્રમે $k_1$ અને $k_2$ છે જેમને સમાન બળથી ખેંચેલી છે. એવું જાણવા મળ્યું કે $S_2$ સ્પ્રિંગ કરતા $S_1$ સ્પ્રિંગ પર થતું કાર્ય વધુ હોય છે.View Solution
વિધાન $1$ : જો સમાન મૂલ્યથી ખેંચવામાં આવે તો $S_1$ પર થતું કાર્ય જે $S_2$ પર થતા કાર્ય કરતા વધારે છે. વિધાન $2 : k_1 < k_2$
- 6$2\,m$ લંબાઇ ધરાવતા સાદા લોલકને $60^°$ ના ખૂણે મુકત કરતા,સમતોલન સ્થાન પાસે ગોળાનો વેગ .......... $m/s$ હશે.View Solution
- 7View Solutionસ્થિતિઊર્જામાં ઘટાડો કઇ પરિસ્થિતિમાં થાય?
- 8એક $0.2 \;kg$ નાં બોલને શિરોલંબ દિશામાં ઉપર તરફ હાથનાં બળ વડે ફેકવામાં આવે છે. બળ લગાવતી વખતે હાથ $0.2\; m$ ખસે છે અને બોલ $2\; m$ ઊંંચાઈએ પહોંચે છે તો બળનું મૂલ્ય શોધો. ($g =10 m / s ^{2}$ લો)View Solution
- 9બે સમાન ગોળાઓ $A$ અને $B$ અનુક્રમે $0.5 \;m/s$ તથા $ -0.3 \;m/s $ ના વેગથી એક પરિમાણમાં ગતિ કરતાં સ્થિતિસ્થાપક અથડામણ અનુભવે છે. અથડામણ પછી ગોળા $ B$ અને ગોળા $A$ ના વેગ અનુક્રમે કેટલા થાય?View Solution
- 10$5 \times 10^{3} \,kg$નો પદાર્થ $2\, m / s$ના વેગથી ગતિ કરીને $15 \times 10^{3} \,kg$ દળના સ્થિર પદાર્થ સાથે અથડાઈને ચોંટી જાય તો તંત્રમાં ગુમાવેલી ગતિ ઊર્જા શોધો. ($KJ$ માં)View Solution
