ગામાં વિકિરણની તીવ્રતા $36mm$ અંતર કાપ્યા પછી આઠમાં ભાગનાી થઇ જાય છે. તો કેટલા .....$mm$ અંતર કાપ્યા પછી તીવ્રતા અડઘી થાય ?
AIEEE 2005, Diffcult
b
(b)\(I' = I\,{e^{ - \mu x}}\) ==> \(x = \frac{1}{\mu }{\log _e}\frac{I}{{I\,'}}\) (where \(I \) = original intensity, \(I'\) = changed intensity)
\(36 = \frac{1}{\mu }{\log _e}\frac{I}{{I/8}}\) = \(\frac{3}{\mu }{\log _e}2\) ....\((i)\)
\(x = \frac{1}{\mu }{\log _e}\frac{I}{{I/2}}\) \( = \frac{1}{\mu }{\log _e}2\) .....\((ii)\)
From equation \((i)\) and \((ii),\) \(x = 12\,mm\).
(b)\(I' = I\,{e^{ - \mu x}}\) ==> \(x = \frac{1}{\mu }{\log _e}\frac{I}{{I\,'}}\) (where \(I \) = original intensity, \(I'\) = changed intensity)
\(36 = \frac{1}{\mu }{\log _e}\frac{I}{{I/8}}\) = \(\frac{3}{\mu }{\log _e}2\) ....\((i)\)
\(x = \frac{1}{\mu }{\log _e}\frac{I}{{I/2}}\) \( = \frac{1}{\mu }{\log _e}2\) .....\((ii)\)
From equation \((i)\) and \((ii),\) \(x = 12\,mm\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વિર્વતનમાં $660 nm$ તરંગલંબાઇની પ્રથમ ન્યૂનતમ .......$\mathop A\limits^o $ તરંગલંબાઇના પ્રથમ અધિકતમ સાથે સંપાત થાય?View Solution
- 2$\lambda$ તરંગલંબાઇનો એક સમાંતર પ્રકાશ પુંજ $d$ પહોળાઇની એક સિંગલ સ્લિટ લંબરૂપે આપાત થાય છે. વિવર્તન ભાત એ સ્લિટથી $ D $ અંતરે મૂકેલા પડદા પર મળે છે. મધ્ય તેજસ્વી બેન્ડથી કેટલા અંતરે દ્વિધ્રુવીય અપ્રકાશીત બેન્ડ મળશે, તે શેના વડે આપવામાં આવે છે?View Solution
- 3View Solutionજ્યારે માણસની આંખ કેવી વસ્તુ પર કેન્દ્રિત થાય ત્યારે તેના આંખના સામાન્ય સ્નાયુઓ ન્યૂનત્તમ ખUચાયેલા હોય છે..
- 4$I$ અને $4I$ તીવ્રતા ધરાવતા બે પ્રકાશ કિરણપુંજો પડદા ઉપર શલાકાઓ ઉત્પન્ન કરે છે. બે કિરણપૂંજો વચ્ચેનો કળા તફાવત $A$ બિંદુએ $\pi / 2$ અને બિંદુ $B$ આગળ $\pi / 3$ છે. પરિણામી તીવ્રતાઓ વચ્ચેનો તફાવત $x I$ છે. $x$ નું મૂલ્ય .......... છે.View Solution
- 5યંગના પ્રયોગમાં એક સ્લીટ દ્વારા એકરંગી પ્રકાશ એ સ્લીટ $S_1$ અને $S_2$ ને પ્રકાશિત કરવા માટે વપરાય છે. વ્યતિકરણ ભાત પડદા પર મેળવવામાં આવે છે. શલાકાની ભાત $ w$ છે. હવે જો $t $ જાડાઈ અને વક્રીભવનાંક $\mu$ ધરાવતી માઈકાની શીટને બે સ્લીટમાંથી એક સ્લીટની આગળ નજીક મુકવામાં આવે છે. હવે શલાકાની ભાત $w'$ છે. તો ......View Solution
- 6એક પડદાની સામે એક પ્રકાશનો સ્ત્રોત મૂકેલો છે. પડદા પર તેની તીવ્રતા $I$ છે. બે પોલેરોઇડ્સ ${P}_{1}$ અને ${P}_{2}$ ને પ્રકાશના સ્ત્રોત અને પડદા વચ્ચે એવી રીતે મૂકવામાં આવે છે કે જેથી પડદા પર પ્રકાશની તીવ્રતા ${I} / 2$ મળે, તો ${P}_{2}$ ને કેટલા ડિગ્રીના ખૂણે ભ્રમણ કરાવવો જોઈએ કે જેથી પડદા પર પ્રકાશની તીવ્રતા $\frac{3 I}{8}$ મળે?View Solution
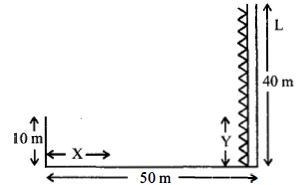
- 7$50\,cm$ પહોળાઈ ધરાવતી નદીના કિનારા પર બહુમાળી ઈમાતરત છે દીવાદાંડીના ટાવરની ઊંચાઈ $40\,m$ છે $10\,m$ ઊંચાઈથી માણસને દીવાદાંડી નો પ્રકાશ પાણીની સપાટીથી ધ્રુવીભૂત થઈને દેખાય છે તે ઇમારતથી $x$ અંતરે થી આવતો પ્રકાશની તીવ્રતા લઘુતમ છે તે દીવાદાંડી પર રહેલા $y$ ઊંચાઈના બ્લબમાંથી આવતા પ્રકાશની તીવ્રતા બરાબર છે તો $x$ અને $y$ ના મૂલ્યો (પાણીનો વક્રીભવનાંક $ \simeq \frac{4}{3})$) છે.View Solution
- 8$1.45 $ વક્રીભવનાંક ધરાવતી પ્લાસ્ટિકની પાતળી (થીન) ફીલ્મને વ્યતિકરણ પામતા તરંગના માર્ગમાં આવે તો, મધ્ય શલાકા પાંચ શલાકાઓ જેટલા અંતરે ખસે છે. જો પ્રકાશની તરંગલંબાઈ $5890\, Å$ હોય તો ફીલ્મની જાડાઈ શોધો.View Solution
- 9$0.1\, \mu m$ પહોળાઈ ધરાવતાં છિદ્ર (પીન હોલ) પર સૂર્ય પ્રકાશ આપાત કરતાં મળતી વિવર્તન ભાત ધ્યાનમાં લો. જે છિદ્રનો વ્યાસ થોડોક વધારીએ તો વિવર્તન ભાત પર એવી રીતે અસર થશે કે ....... .View Solution
- 10$0.1 \,mm$ અંતરે રહેલા બે બિંદુને જયારે $6000\, Å$ તરંગલંબાઇ વાપરવામાં આવે,ત્યારે માઇક્રોસ્કોપથી અલગ જોઇ શકાય છે.તો ........$mm$ અંતરે રહેલા બે બિંદુને જયારે $4800 \,Å$ તરંગલંબાઇ વાપરવામાં આવે,ત્યારે માઇક્રોસ્કોપથી અલગ જોઇ શકાય?View Solution
