એક પડદાની સામે એક પ્રકાશનો સ્ત્રોત મૂકેલો છે. પડદા પર તેની તીવ્રતા $I$ છે. બે પોલેરોઇડ્સ ${P}_{1}$ અને ${P}_{2}$ ને પ્રકાશના સ્ત્રોત અને પડદા વચ્ચે એવી રીતે મૂકવામાં આવે છે કે જેથી પડદા પર પ્રકાશની તીવ્રતા ${I} / 2$ મળે, તો ${P}_{2}$ ને કેટલા ડિગ્રીના ખૂણે ભ્રમણ કરાવવો જોઈએ કે જેથી પડદા પર પ્રકાશની તીવ્રતા $\frac{3 I}{8}$ મળે?
JEE MAIN 2021, Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રકાશીય ઉપકરણમાં વપરાતા પ્રકાશની તરંગલંબાઈ ${\lambda _1} = 4000 \mathring A$ અને ${\lambda _2} = 5000 \mathring A $ છે, તો તેમની વિભેદન શક્તિનો ગુણોત્તર (${\lambda _1}$ અને ${\lambda _2})$ ને અનુરૂપ) કેટલો મળે?View Solution
- 2બે પોલેરોઈડની અક્ષ એકબીજાને સમાંતર છે જેથી તેમાંથી નીકળતા પ્રકાશની તીવ્રતા મહત્તમ મળે. તો કોઈ પણ એક પોલેરોઈડને કેટલા $^o$ ના ખૂણે ફેરવવો જોઈએ કે જેથી તેમાંથી નીકળાતા પ્રકાશની તીવ્રતા અડધી થાય?View Solution
- 3View Solutionતરંગ એક જગ્યાએથી બીજી જગ્યાએ શેનું વહન કરે છે?
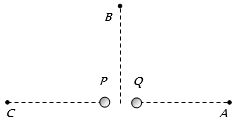
- 4$p$ અને $Q$ ઉદગમ સમાન તીવ્રતા ધરાવતા $20\,m$ તરંગલંબાઈ ધરાવતા તરંગો ઉત્પન્ન કરે છે. $p$ અને $Q$ વચ્ચેનું અંતર $5\,m$ છે. $P$ ની કળા $Q$ કરતા $90^{\circ}$ આગળ છે. $PQ$ ના મધ્યબિંદુથી સમાન અંતરે $A,B$ અને $C$ છે. $A,B,C$ આગળ તીવ્રતાનો ગુણોતર કેટલો થાય?View Solution
- 5$0.2 \mathrm{~mm}$ પહોળાઈ ધરાવતી સ્લિટ પરથી $400 \mathrm{~nm}$ તરંગલંબાઈ ધરાવતા પ્રકાશથી વિવર્તન માટે મળતી વિવર્તન ભાત ને $100 \mathrm{~cm}$ કેન્દ્રલંબાઈના બહિર્ગોળ લેન્સની મદદથી ફોકલ સમતલ (મુખ્ય સમતલ) પર કેન્દ્રિત (ફોક્સ) કરવામાં આવે છે. પહેલાં દ્વિતીય મહત્તમોની પહોળાઈ_________થશે.View Solution
- 6આદર્શ રીતે યંત્રના બે સ્લીટના પ્રયોગમાં, $ t $ જાડાઈ ધરાવતી કાચની પ્લેટ ($\mu=1.5$) ને વ્યતિકરણ કરતા રંગની વચ્ચે મૂકવામાં આવે છે. ($\lambda$ તરંગલંબાઈ), અહી તીવ્રતા કે જ્યાં જે સ્થાન પર પહેલા કેન્દ્રીય શલાકા હતી ત્યાં બદલાતી નથી. તો કાચની પ્લેટની ઓછામાં ઓછી જાડાઈ .....View Solution
- 7View Solutionપ્રકાશ તરંગ પ્રકૃતિ ધરાવે છે, કારણ કે.....
- 8યંગના દ્વિ સ્લીટ પ્રયોગમાં વ્યતિકરણ શલાકાઓ મેળવવા માટે પ્રકાશ બીમમાં બે તરંગલંબાઈઓ $6500\, Å $ અને $ 5200 \,Å $ નો સમાવેશ થાય છે. સ્લીટો વચ્ચેનું અંતર $2\, mm $ છે અને સ્લીટોનું સમતલ અને પડદા વચ્ચેનું અંતર $120 \,cm$ છે. બંન્ને તરંગલંબાઈના સુસંગત થવાના કારણે મળતી પ્રકાશિત શલાકાઓનું કેન્દ્રિત મહત્તમ શલાકાથી ઓછામાં ઓછું અંતર શું છે?View Solution
- 9એક સ્લીત ના પ્રયોગમાં થતાં વિવર્તનમાં સફેદ પ્રકાશ વડે $a$ પહોળાયની સ્લીટને પ્રકાશિત કરવામાં આવે છે. લાલ પ્રકાશ ($\lambda = 6500\;\mathring A$) માટે પ્રથમ લઘુત્તમ $\theta = {30^o}$ ખૂણે મળે છે. તો $a$ નું મૂલ્ય કેટલું હશે?View Solution
- 10બે તરંગો $ y_1 = a sin(\omega t) $ અને $ {y_2} = b\cos (\omega t) $ વચ્ચે કળા તફાવત કેટલો થાય?View Solution