ગરમ પાણીનું તાપમાન $ {60^o}C $ થી $ {50^o}C $ થતા $10 min$ લાગે છે,અને તાપમાન $ {50^o}C $ થી ${42^o}C$ થતા $10 min$ લાગે છે.તો વાતાવરણનું તાપમાન ......... $^oC$ હશે?
Diffcult
b
(b) According to Newton's law of cooling
\(\frac{{{\theta _1} - {\theta _2}}}{t} = K\left[ {\frac{{{\theta _1} + {\theta _2}}}{2} - {\theta _0}} \right]\)
In the first case, \(\frac{{(60 - 50)}}{{10}} = K\,\left[ {\frac{{60 + 50}}{2} - {\theta _0}} \right]\)
\(1 = K\,(55 - \theta )\)….\((i)\)
In the second case, \(\frac{{(50 - 42)}}{{10}} = K\,\left[ {\frac{{50 + 42}}{2} - {\theta _0}} \right]\)
\(0.8 = k\,(46 - {\theta _0})\)….\((ii)\)
Dividing \((i)\) by \( (ii)\) , we get \(\frac{1}{{0.8}} = \frac{{55 - \theta }}{{46 - \theta }}\)
or \(46 - {\theta _0} = 44 - 0.8\theta \) ==> \({\theta _0} = {10^o}C\)
(b) According to Newton's law of cooling
\(\frac{{{\theta _1} - {\theta _2}}}{t} = K\left[ {\frac{{{\theta _1} + {\theta _2}}}{2} - {\theta _0}} \right]\)
In the first case, \(\frac{{(60 - 50)}}{{10}} = K\,\left[ {\frac{{60 + 50}}{2} - {\theta _0}} \right]\)
\(1 = K\,(55 - \theta )\)….\((i)\)
In the second case, \(\frac{{(50 - 42)}}{{10}} = K\,\left[ {\frac{{50 + 42}}{2} - {\theta _0}} \right]\)
\(0.8 = k\,(46 - {\theta _0})\)….\((ii)\)
Dividing \((i)\) by \( (ii)\) , we get \(\frac{1}{{0.8}} = \frac{{55 - \theta }}{{46 - \theta }}\)
or \(46 - {\theta _0} = 44 - 0.8\theta \) ==> \({\theta _0} = {10^o}C\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે દ્રવ્યોની ઉષ્મા વાહકતાનો ગુણોત્તર $1 : 2$ છે. તો આજ દ્રવ્યોેના સળીયાની લંબાઇનો ગુણોત્તર $1 : 2$ અને આડછેદના ક્ષેત્રફળનો ગુણોત્તર $2 : 1$ હોય તો તેમના ઉષ્મિય અવરોધનો ગુણોત્તર ........View Solution
- 2View Solutionવાતાવરણના સ્તરો ગરમ કઇ પ્રક્રિયાથી થાય છે?
- 3View Solutionઇન્ફ્રારેડ કિરણો શોધવા માટેનું સાધન
- 4$727^oC$ તાપમાને રહેલ કાળા પદાર્થનો ઉત્સર્જિત પાવર $60\,\, watt$ અને પરિસરનું તાપમાન $227^oC$ છે. જો કાળા પદાર્થનું તાપમાન બદલીને $1227^oC$ કરવામાં આવે, તો ઉત્સર્જિત પાવર ($watt$ માં) કેટલો થશે?View Solution
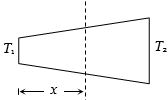
- 5View Solutionઅનિયમિત આડછેદ ધરાવતા વાહકમાંથી ઉષ્મા પસાર થાય છે.તો ઉષ્મા પ્રવાહ વિરુધ્ધ અંતરનો આલેખ.
- 6ત્રણ જુદા જુદા તારાઓ $P, Q$ અને $R$ ના પ્રકાશના અભ્યાસ પરથી જાણવા મળ્યું કે પ્રકાશના $P$ ના વર્ણપટમાં જાંબલી રંગની તીવ્રતા મહત્તમ, $R$ ના વર્ણપટમાં લીલા રંગની તીવ્રતા મહત્તમ અને $Q$ ના વર્ણપટમાં લાલ રંગની તીવ્રતા મહત્તમ છે. જો $P, Q$ અને $R$ ના નિરપેક્ષ તાપમાન અનુક્રમે $T_P , T_Q$ અને $T_R$ હોય, તો ઉપરોક્ત અવલોકનો પરથી તે તારણ કાઢી શકાય છે કેView Solution
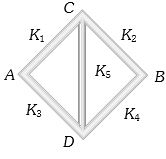
- 7સમાન પરીમાણ ધરાવતા પાંચ સળિયાને આકૃતિ મુજબ જોડેલા છે. $A$ અને $B$ ને જુદાં જુદાં તાપમાને રાખતાં $CD$ માંથી ઉષ્માનું વહન થતું નથી,તોView Solution
- 8એક પદાર્થ $61^{\circ} {C}$ થી $59^{\circ} {C}$ ઠંડો પડવા માટે $4\, {min}$ સમય લગાડે છે. જો આસપાસના વાતાવરણનું તાપમાન $30^{\circ} {C}$ હોય તો પદાર્થ $51^{\circ} {C}$ થી ઠંડો પડી $49^{\circ} {C}$ થવા માટે કેટલો સમય ($min$ માં) લાગશે?View Solution
- 9ગરમ પાણીનું તાપમાન $ {60^o}C $ થી $ {50^o}C $ થતા $10$ min લાગે છે,તો તેની પછીની $10$ min પછી પદાર્થનું તાપમાન ......... $^oC$ શોધો.વાતાવરણનું તાપમાન $ {25^o}C $ છે.View Solution
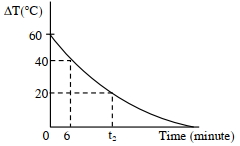
- 10ન્યૂટનનો શીત નિયમ (cooling law) સાબિત કરવાના એક પ્રયોગમાં પાણીનાં અને આસપાસનાં તાપમાનમાં થતા ફેરફાર $(\Delta T)$ અને સમયનો આલેખ દોરવામાં આવેલ છે. પાણીનું પ્રારંભિક તાપમાન $80^{\circ} C$ જેટલું લેવામાં આવે છે. આલેખમાં દર્શાવેલ $t_{2}$ નું મૂલ્ય........થશે.View Solution