$H_2$ ની $I_2$ સાથેની પ્રક્રિયા માટે, $327\,^oC$ પર વેગ અચળાંક $2.5\times 10^{-4}\,dm^3\,mol^{-1}\,s^{-1}$ અને $527\,^oC$ પર $1.0\,dm^3\,mol^{-1}\,s^{-1}$ છે. તો પ્રક્રિયાતી સક્રિયકરણ ઊર્જા ($kJ\,mol^{-1}$ માં) જણાવો. $(R = 8.314\,J\,K^{-1}\,mol^{-1} )$
JEE MAIN 2019, Diffcult
Download our app for free and get started
b
\({H_2}(g)\, + \,{I_2}(g)\, \to \,2HI\,(g)\)
\({H_2}(g)\, + \,{I_2}(g)\, \to \,2HI\,(g)\)
Apply Arrhenius equation
\(\log \,\frac{{{K_2}}}{{{K_1}}}\, = \,\frac{{{E_a}}}{{2.303\,R}}\left( {\frac{1}{{600}} - \frac{1}{{800}}} \right)\)
\(\log \,\frac{1}{{2.5 \times {{10}^{ - 4}}}}\, = \,\frac{{{E_a}}}{{2.303 \times 8.31}}\,\left( {\frac{{200}}{{600 \times 800}}} \right)\)
\(\therefore \,\,{E_a}\, \approx \,166\,\,kJ\,/\,mol\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solution..............નું મૂલ્ય જાણતા હોય તો કોઈ પણ રાસાયણિાક પ્રક્રિયાની સક્રિયકરણ શક્તિની ગણાતરી કરી શકાય છે.
- 2$KClO _3+6 FeSO _4+3 H _2 SO _4 \rightarrow KCl +3 Fe _2\left( SO _4\right)_3+3 H _2 O$View Solution
ઉપરોક્ત પ્રક્રિયાનો અભ્યાસ $FeSO _4$ ની સાંદ્રતાનું નિરીક્ષણ કરીને $300\,K$ પર કરવામાં આવ્યો હતો, જેમાં પ્રારંભિક સાંદ્રતા $10\,M$ હતી અને અડધા કલાક પછી $8.8\,M$ થઈ ગઈ હતી. $Fe _2\left( SO _4\right)_3$ ના ઉત્પાદનનો વેગ એ $..........\,\times 10^{-6}\,mol\,L ^{-1}\,s ^{-1}$ છે.
- 3એક વાયરૂપ પ્રક્રિયાનો વેગ $r = K\,[x]\, [y]$ છે. જો એકાએક પાત્રનુ કદ ઘટાડીને શરૂઆતના કદથી $1/4$ જેટલુ કરવામાં આવે તો પ્રક્યિાનો વેગ ............View Solution
- 4પ્રથમ ક્રમ ની પ્રકિયા માટે અચલ વેગ $2.303 \times 10^{-3} \;\mathrm{s}^{-1} .$ છે $40 \mathrm{g}$ પ્રકીયક ને $10\; \mathrm{g}$ પ્રકિયા થવા માટે લાગતો સમય........$s$View Solution
[અહી આપેલ $\left.\log _{10} 2=0.3010\right]$
- 5View Solutionનીચે પૈકી કયું વિધાન સાચું છે?
- 6જો પ્રક્રિયકની સાંદ્રતા $a$ હોય તો $100\%$ શૂન્યક્રમની પ્રક્રિયા પૂરી કરવા માટે કેટલો સમય લાગશે ?View Solution
- 7નિશ્ચિત વાયુમય પ્રક્રિયા માટે તેના તાપમાનમાં $10\,^oC$ નો વધારો $25\,^oC$ થી $35\,^oC$ સુધી કરવામાં આવે છે. તો પ્રક્રિયાનો દર બમણો થાય છે તો સક્રિયકરણ ઊર્જાનું મૂલ્ય શું થશે?View Solution
- 8જ્યારે તાપમાન વધીને $300\,K$ થી $310 \,K$ થાય ત્યારે પ્રક્રિયાનો દર $2.3 $ ગણુ વધે છે. જો $300 \,K$ એ દર અચળાંક $x$ હોય તો $310 \,K$ એ દર અચળાંક....... જેટલું થાય છે.View Solution
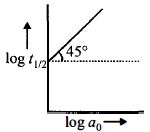
- 9પ્રક્રિયા $A \to$ નીપજો માટે $log\,t_{1/2}$, વિરુદ્ધ $log\,a_0$ નો આલેખ આકૃતિમાં દર્શાવ્યો છે. જો $A$ ની શરૂઆતની સાંદ્રતા $a_0,$, વડે દર્શાવવામાં આવે તો પ્રક્રિયાની ક્રમ જણાવો.View Solution
- 10પ્રથમ ક્રમની વાયુમય પ્રક્રિયા માટે સંકલીત વેગ નિયમ ક્યા સમીકરણથી દર્શાવી શકાય છે. (જ્યાં $P_i=$ પ્રારંભિક દબાણ, $\mathrm{P}_{\mathrm{t}}=\mathrm{t}$ સમયે કુલ દબાણ)View Solution