હાઈડ્રોજન પરમાણુ માટે બોહરની દ્વિતીય કક્ષાની ત્રિજ્યા .......... $\mathop A\limits^o $.
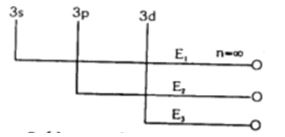
(પ્લાંક અચળાંક $ h = 6. \times 10^{-34}\, Js\,;$ ઇલેક્ટ્રોનનું દળ $= 9.1091 \times 10^{-31}\, kg\,;$ ઇલેક્ટ્રોનનો વિજભાર $e= 1.60210 \times 10^{-19}\, C\,;$ શૂન્યાવકાશની પારગમ્યતા $\epsilon _0 = 8.854185 \times 10^{-12} \,kg^{-1} \,m^{-3} A^2$)
JEE MAIN 2017, Medium
Download our app for free and get started
d
According to Bohr's theory
According to Bohr's theory
\(r =0.529 \times \frac{n^{2}}{Z} \mathop A\limits^o \)
\( = 0.529 \times \frac{{{2^2}}}{1} = 2.116{\mkern 1mu} \,\mathop A\limits^o \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો તમે $1050\,kg$ દળની કારમાં $90\,km/h$ ની ઝડપથી ગતિ કરતા હોય અને કારના વેગની અનિશ્ચિતતા $1\,\%$ હોય, તો તેના સ્થાનની અનિશ્ચિતતા કેટલી થશે ?View Solution
- 2એકઇલેક્ટ્રોનની ઊર્જા નીચે પ્રમાણે દર્શાવેલ છે.View Solution
$E =- 2.178 \times 10^{-18}\,J \, \left( {\frac{{{Z^2}}}{{{n^2}}}} \right)$ તો હાઈડ્રોજન પરમાણુમાં રહેલા ઇલેક્ટ્રોનને $n = 1$ થી $n = 2$ શક્તિસ્તરમાં ઉતેજિત કરવા માટે કેટલી તરંગલંબાઈ પ્રકાશની જરૂર પડશે ?
$(h = 6.62 \times 10^{-34} \,J\,s , c = 3.0 \times 10^8 \,ms^{-1})$
- 3$n=4$ સાથે કોશમાં ઈલેકટ્રોનોની મહત્તમ સંખ્યા સમાવી શકાય તે શોધો.View Solution
- 4$(A)\, n = 5, m_l= + 1$ $(B)\, n =2, l =1, m_l= -1, m_s = -1/2$ આપેલ છે . તો $(A)$ અને $(B)$ માં આપેલ ક્વોન્ટમ આંક મુજબ પરમાણુમા ઇલેક્ટ્રોનની મહતમ સંખ્યા અનુક્રમે જણાવોView Solution
- 5View Solutionનીચેનામાંથી શામાં ઇલેક્ટ્રોનની કક્ષકો બિનગોલીય છે ?
- 6જો હાઇડ્રોજન પરમાણુની આયનીકરણ ઊર્જા $E$ હોય, તો $Li^{2+}$ ની આયનીકરણ ઊર્જા ............ $\mathrm{E}$ થશે.View Solution
- 7$(n = 4)$ ઈલેકટ્રોન્સ માટે $m$ કુલ મૂલ્ય થશે ?View Solution
- 8ધરા અવસ્થામાંથી $n$ મી કક્ષામાં ઉત્સર્જન પામેલા એક ઇલેક્ટ્રોનની ઊર્જા કેટલી થશે?View Solution
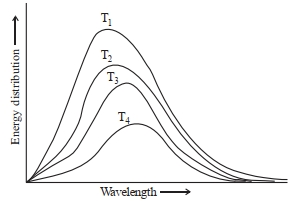
- 9ચાર જુદા જુદા તાપમાનો પર એક આદર્શ કાળો પદાર્થ $(ideal\,black\,body)$ નો વર્ણપટ (સ્પેકટ્રમ)નીચે આકૃતિમાં દર્શાવેલ છે. નીચે આપેલામાંથી સાચું/નો ની સંખ્યા $...........$ છે.View Solution
$A.$ $T _4 > T _3 > T _2 > T _1$
$B.$ કણો ધરાવતો કાળો પદાર્થ સાંદી સંવાદી ગતિ નું પાલન કરે છે.
$C.$ તાપમાનમાં વધારો થતા વર્ણપટનો પીક ટૂંકી તરંગલંબાઈ તરફ ખસે છે.
$D.$ $\frac{T_1}{v_1}=\frac{T_2}{v_2}=\frac{T_3}{v_3} \neq$ અચળ
$E.$ શક્તિના ક્વોન્ટીકરણનો ઉપયોગ કરીને આપેલ વર્ણપટને સમજાવી શકાય છે.
- 10$H$ પરમાણુ માટે જુદી જુદી પેટા કક્ષકોમાંથી ઈલેકટ્રોનને દૂર થવા માટે જરૂરી ઊર્જા નીચે આપેલી છે ? આ ઊર્જાનો ક્રમ શું થશે ?View Solution
