હાઇડ્રોજન પરમાણુમાં ધરા-સ્થિતિમાં રહેલા ઇલેકટ્રોનને $\lambda =975 \;\mathring A$ તરંગલંબાઇના એકરંગી વિકિરણ વડે ઉત્તેજિત કરવામાં આવે છે. પરિણામી વર્ણપટમાં વર્ણપટ રેખાઓની સંખ્યા કેટલી હશે?
AIPMT 2014, Medium
c
Energy of the photon, \(E=\frac{n c}{\lambda}\)
Energy of the photon, \(E=\frac{n c}{\lambda}\)
\(E=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{975 \times 10^{-10}} \mathrm{J}\)
\(=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{975 \times 10^{-10} \times 1.6 \times 10^{-19}} \mathrm{eV}=12.75 \mathrm{eV}\)
After absorbing a photon of energy \(12.75\,eV\), the electron will reach to third excited state of energy \(-0.85\) eV, since energy difference corresponding to \(n=1\) and \(n=4\) is \(12.75 \mathrm{eV}\)
\(\therefore\) Number of spectral lines emitted
\(=\frac{(n)(n-1)}{2}=\frac{(4)(4-1)}{2}=6\)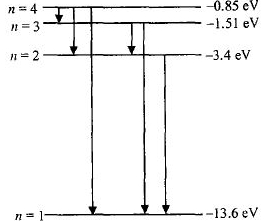
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1હાઇડ્રોજન જેવા પરમાણુમાં ઇલેક્ટ્રૉન $M- $શેલ (કક્ષા) માંથી $L-$ શેલ (કક્ષા) માં જાય છે. ઉત્સર્જતા વિકિરણની તરંગલંબાઈ $\lambda$ છે. ઇલેક્ટ્રૉન $N-$ શેલ (કક્ષા) માંથી $L-$ શેલ (કક્ષા) માં જાય તો ઉત્સર્જતા વિકિરણની તરંગલંબાઈ કેટલી હશેView Solution
- 2View Solutionસ્થિર રહેલા એક હાઇડ્રોજન પરમાણુમાં એક ઇલેકટ્રોન પાંચમી કક્ષામાંથી ધરા-સ્થિતિમાં આવે છે. ફોટોન ઉત્સર્જનના પરિણામે પરમાણુને મળતો વેગ કેટલો હશે?
- 3બે ઘટકોની $ K_\alpha$ રેખાઓની તરંગ લંબાઈ અનુક્રમે $250 $ અને $179 \,pm$ છે. આ ઘટકો વચ્ચેનો ઘટક આંક શ્રેણીમાં ......હશે.View Solution
- 4એક કાલ્પનિક અણુંમાં ઊર્જાના ત્રણ સ્તરો છે. જેની ધરા અવસ્થાની ઉર્જા $E_1 = - 8\, eV$. બીજા બે સ્તરોની ઉર્જા $E_2 = - 6\, eV$ અને $E_3 = - 2\, eV$ છે. તો અણુના વર્ણપટ્ટમાં કઈ તરંગલંબાઈનું ($nm$ માં) ઉત્સર્જન થશે નહી?View Solution
- 5હાઇડ્રોજનમાં ધરા- સ્થિતિમાં રહેલા ઇલેકટ્રોનની ત્રિજયા $1.06 \,Å$ છે,તો $10$ મી કક્ષામાં રહેલા ઇલેકટ્રોનની ત્રિજયા કેટલા .......$\mathop A\limits^o $ હશે?View Solution
- 6$He ^{+1}$ આયનમાં $3^{\text {rd }}$ કક્ષામાં રહેલા ઇલેક્ટ્રોનની દ-બ્રોગ્લી તરંગલંબાઈ ($\mathring A$ માં) કેટલી થાય ?View Solution
- 7હાઈડ્રોજન પરમાણુની પ્રથમ કક્ષાની ત્રિજ્યા $ 0.5 \,Å $ અને ઈલેક્ટ્રોનની ઝડપ $2.2 ×10^6\, m /sec$ છે. તો ઈલેક્ટ્રોન ની ગતિના લીધે પ્રોટોન પાસે ઉદ્દભવતું ચુંબકીય પ્રેરણ......$Tesla$ શોધો.View Solution
- 8જો $He$ પરમાણુમાંથી એક ઈલેક્ટ્રોન દૂર કરવા માટે $29.5\,eV$ ઊર્જાની જરૂર પડતી હોય તો $He $ને $\alpha$ કણ બનાવવા .......... $eV$ ઊર્જાની જરૂર પડશે ?View Solution
- 9હાઈડ્રોજન પરમાણુમાં ધરાસ્થિતિમાં રહેલા ઇલેક્ટ્રોનની ઊર્જા $-13.6$ છે.તો ચોથી કક્ષામાં રહેલા ઇલેક્ટ્રોનની ઝડપ શોધો.View Solution
- 10જો $f_1, f_2$ અને $f_3$ અનુરૂપ ધાતુઓનો $K_\alpha, K_\beta$ અને $L_\alpha X-rays$ હોય તો.....View Solution
