હાઇડ્રોજન પરમાણુમાં ઇલેકટ્રોન ત્રીજી ઉત્તેજિત સ્થિતિમાંથી બીજી ઉત્તેજિત સ્થિતિમાં સંક્રાતિ કરે ત્યારે અને હાઇડ્રોજન પરમાણુમાં ઇલેકટ્રોન બીજી ઉત્તેજિત સ્થિતિમાંથી પ્રથમ ઉત્તેજિત સ્થિતિમાં સંક્રાતિ કરે ત્યારના બંને કિસ્સાની તરંગલંબાઇઓનો ગુણોત્તર $\lambda_1 :\lambda_2$ કેટલો થાય?
AIPMT 2012, Diffcult
d
According to Rydberg formula
According to Rydberg formula
\(\frac{1}{\lambda}=R\left[\frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{2}}\right]\)
In first case, \(n_{f}=3, n_{i}=4\)
\(\therefore \quad \frac{1}{\lambda_{1}}=R\left[\frac{1}{3^{2}}-\frac{1}{4^{2}}\right]=R\left[\frac{1}{9}-\frac{1}{16}\right]=\frac{7}{144} R\) .... \((i)\)
In second case, \(n_{f}=2, n_{i}=3\)
\(\therefore \quad \frac{1}{\lambda_{2}}=R\left[\frac{1}{2^{2}}-\frac{1}{3^{2}}\right]=R\left[\frac{1}{4}-\frac{1}{9}\right]=\frac{5}{36} R\) .... \((ii)\)
Divide \((ii)\) by \((i)\), we get
\(\frac{\lambda_{1}}{\lambda_{2}}=\frac{5}{36} \times \frac{144}{7}=\frac{20}{7}\)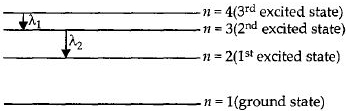
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પાશ્વન શ્રેણી સાથે સંકળાયેલ લાંબામાં લાંબી તરંગલંબાઈ. . . . . . હશે. $\left(\mathrm{R}_{\mathrm{H}}=1.097 \times 10^7 \mathrm{SI}\right.$ એકમ $)$View Solution
- 2View Solutionજ્યારે ધાતુ સપાટી પર ઉચ્ય ઊર્જા ધરાવતા ઇલેકટ્રોનનો મારો ચલાવવામાં આવે, ત્યારે તેમાંથી .......... ઉત્સર્જિત થાય છે.
- 3$5 × 10^{-3}\, m$ જાડાઈના સોનાની ફિલ્મ પસાર કર્યા પછી ક્ષ કિરણની પ્રારંભિક તીવ્રતા કરતાં ક્ષ કિરણ પુંજની તીવ્રતા $36.8\%$ જેટલી ઘટે તો તેનો શોષણ ગુણાંક .......$m^{-1}$ છે.View Solution
- 4હાઈડ્રોજન વર્ણપટમાં લ્યુમેન શ્રેણીની છેલ્લી રેખાની તરંગ લંબાઈ $911\, Å$ છે. ઘટકનો પરમાણ્વિય આંક કે જે $0.7\, Å$ ન્યૂનત્તમ તરંગ લંબાઈના ક્ષ કિરણ લાક્ષણિકતા આપાત થાય તો......View Solution
- 5હાઇડ્રોજન અણુમાં એક ઇલેક્ટ્રોન ન્યુક્લિયસની ફરતે $0.528 \;\mathring A$ ની કક્ષામાં $2.18 \times 10^{6} \;m / s$ ના વેગથી ગતિ કરે છે. તો ઇલેક્ટ્રોનનો પ્રવેગ કેટલો થશે?View Solution
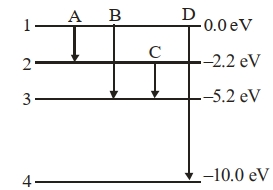
- 6પરમાણુના ઉર્જા સ્તરો આકૃતિમાં દર્શાવેલ છે. $124.1\,nm$ તરંગ લંબાઇના ફોટોનના ઉત્સર્જનમાં આમાંથી કઈ સંક્રાતિ ઉદ્દભવશે ?View Solution
$\text { ( } h =6.62 \times 10^{-34}\,Js)$ આવેલું છે.
- 7View Solutionહાઇડ્રોજન પરમાણુમાં જ્યારે ઇલેકટ્રૉન ધરા સ્થિતિમાંથી ઉત્તેજિત અવસ્થામાં જાય છે ત્યારે ઇલેકટ્રૉનની ...
- 8બોહરના મોડેલમાં $R _1$ એ ઇલેક્ટ્રોનની બીજી સ્થિર ભ્રમણકક્ષાની ત્રિજ્યા અને $R_2$ એ ચોથી સ્થિર ભ્રમણકક્ષાની ત્રિજ્યા છે. ગુણોત્તર $\frac{ R _1}{ R _2}$ કેટલો હશે?View Solution
- 9જ્યારે $0.50\; \mathring A$ ના ક્ષ-કિરણોને ધાતુ પર આપાત કરવામાં આવે છે, ત્યારે જણાય છે કે $k\,shell$ ના ફોટોઈલેકટ્રોન એ $2 \times 10^{-3}\,tesla$ ચુંબકીય ક્ષેત્રમાં રહેલા $23\,mm$ ત્રિજ્યાના વર્તુળ તરફ ગતિ કરે છે. આ ચુંબકીય ક્ષેત્રએ ફોટો ઈલેક્ટ્રોનની બંધન ઉર્જા $..........\, keV$View Solution
- 10હાઈડ્રોજન પરમાણુ ઉત્તેજીત અવસ્થામાંથી $\lambda$ તરંગલંબાઈ ધરાવતા ફોટોનનું ઉત્સર્જન કરીને ધરા સ્થિતિમાં આવે છે. ઉત્તેજીત અવસ્થા માટે મુખ્ય કવોન્ટમ નંબર '$n$' નું મૂલ્ય $.........$ થશે. ($R :$ રીડબર્ગ અચળાંક)View Solution
