જ્યારે $0.50\; \mathring A$ ના ક્ષ-કિરણોને ધાતુ પર આપાત કરવામાં આવે છે, ત્યારે જણાય છે કે $k\,shell$ ના ફોટોઈલેકટ્રોન એ $2 \times 10^{-3}\,tesla$ ચુંબકીય ક્ષેત્રમાં રહેલા $23\,mm$ ત્રિજ્યાના વર્તુળ તરફ ગતિ કરે છે. આ ચુંબકીય ક્ષેત્રએ ફોટો ઈલેક્ટ્રોનની બંધન ઉર્જા $..........\, keV$
Diffcult
a
(b)
(b)
The velocity of the photoelectrons is found by the relation :
\(e v B=m \frac{v^2}{R} \text { or } v=\frac{e}{m} B R\)
The kinetic energy of the hotoelectrons is
\(K =\frac{1}{2} m v^2=\frac{1}{2} \frac{e^2 B^2 R^2}{m}\)
\(=\frac{1}{2} \frac{\left(1.6 \times 10^{-19}\right)^2\left(2 \times 101^{-2}\right)^2\left(23 \times 10^{-3}\right)^2}{\left(9.1 \times 10^{-31}\right)}\)
\(=2.97 \times 10^{-15}\,J\)
\(=\left(2.97 \times 10^{-15}\right) \frac{1}{1.6 \times 10^{-19}}=18.36\,KeV\)
The energy of the incident photon is \(E_v=\frac{h c}{\lambda}=\frac{12.4}{0.50}=24.8\,KeV\)
The binding energy is the difference between these two values:
\(B E=E_v-K=24.8 - 18.6- 6.2\,keV\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionહાઇડ્રોજનના વર્ણપટમાં લાઇમન અને બામર શ્રેણીઓની લાંબામાં લાંબી તરંગલંબાઇઓનો ગુણોત્તર શું થશે?
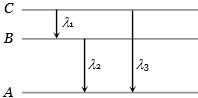
- 2ચોક્કસ અણુના $A, B, C$ ઉર્જા સ્તરો માટે વધતી ઊર્જાના મૂલ્યો ${E_A} < {E_B} < {E_C}$ છે. જો ${\lambda _1},\;{\lambda _2},\;{\lambda _3}$ અનુક્રમે $C$ થી $B, \;B$ થી $A$ અને $C$ થી $A$ સંક્રાતિ દરમિયાન ઉત્સર્જન થતી તરંગલંબાઇ હોય, તો કયું વિધાન સાચું થાય?View Solution
- 3બોહર મોડલમાં પ્રથમ ક્ક્ષા ની ત્રિજયા ${r_0}$ હોય તો, ત્રીજી કક્ષાની ત્રિજ્યાView Solution
- 4View Solutionઆપેલ પ્રવેગિત વોલ્ટેજ આગળ ક્ષ કિરણો ટ્યૂબમાં ક્ષ કિરણો ઉત્પન્ન થાય છે. સતત ક્ષ કિરણોની તરંગ લંબાઈનું મૂલ્ય .......હશે.
- 5$U\left( r \right) = \frac{1}{2}k{r^2}$ ના કેન્દ્રીય સ્થિતિમાન ક્ષેત્રમાં એક વર્તુળાકાર કક્ષામાં $m$ દ્રવ્યમાન વાળો એક કણ ગતિ કરે છે.જો ક્વોન્ટાઇઝેશન શરતો લગાડવામાં આવે તો શક્ય કક્ષકો અને તેના ઊર્જાસ્તરો એ ક્વોન્ટમ ક્રમ (સંખ્યા) $ n$ સાથે ______ થી ચલે છે.View Solution
- 6એક ઈલેક્ટ્રોન ઘન વિદ્યુતભાર ધરાવતા ન્યુક્લિયસને ફરતે વર્તુળ માર્ગ પર ભ્રમણ કરે છે. ઈલેક્ટ્રોનની કુલ ઉર્જા ($E$) અને તેની સ્થિતિઉર્જા ($U$) વચ્ચેનો સાચો સંબંધ. . . . . . હશે.View Solution
- 7View Solutionધરાસ્થિતિ એ રહેલા હાઈડ્રોજન પરમાણુની કક્ષામાં રહેલા ઇલેક્ટ્રોનની ઝડપ કેટલી છે ?
- 8$Li ^{++}$ આયનમાંના ઇલેક્ટ્રોનનને પ્રથમ કક્ષામાંથી ત્રીજી બોહર કક્ષામાં સંક્રાતિ કરાવવા માટે કેટલી ઊર્જાની ($eV$ માં) જરૂર પડે?View Solution
- 9ક્ષ કિરણ ટ્યૂબમાં જ્યારે પ્રવેગિત વોલ્ટેજ $ 10\, kV $ થી $20\, kV$ સુધી વધે તો $ K_\alpha$ રેખાની તરંગલંબાઈ અને સતત વર્ણપટના નીચેના છેડા વચ્ચેની જગ્યા ત્રણ ગણી વધે છે. ટાર્ગેંટ ઘટકનો પરમાણ્વિય આંક .....છે.View Solution
- 10$B$ ચુંબકીયક્ષેત્રની અસર હેઠળ ગતિ કરતા $m$ દળ અને $q$ વિજભાર ધરાવતા કણ પર બોહર મોડલ લાગુ પાડતાં વિજભારિત કણના $n$ માં સ્તરની ઉર્જા કેટલી હશે?View Solution
