હાઈડ્રોજન વર્ણપટમાં લાઇમન શ્રેણીની મહતમ અને લઘુતમ તરંગલંબાઈનો તફાવત $304\,\mathring {A}$ હોય તો પાશ્ચન શ્રેણીમાં આ તફાવત $........... \,\mathring {A}.$
JEE MAIN 2020, Diffcult
a
\(\lambda=\frac{ c }{\left(\frac{1}{ n _{1}^{2}}-\frac{1}{ n _{2}^{2}}\right)}\)
\(\lambda=\frac{ c }{\left(\frac{1}{ n _{1}^{2}}-\frac{1}{ n _{2}^{2}}\right)}\)
for lyman series
\(\lambda_{1}=\frac{ c }{\frac{1}{1^{2}}-\frac{1}{\infty^{2}}}= c ( n =\infty\) to \(n =1)\)
\(\lambda_{2}=\frac{c}{\frac{1}{1^{2}}-\frac{1}{2^{2}}}=\frac{4 c}{3}(n=2\) to \(n=1)\)
\(\Delta \lambda=\lambda_{2}-\lambda_{1}=\frac{ c }{3}=304 A \Rightarrow c =912 A\)
for paschen series
\(\lambda_{1}=\frac{ c }{\frac{1}{3^{2}}-\frac{1}{\infty^{2}}}=9 c ( n =\infty\) to \(n =3)\)
\(\lambda_{2}=\frac{ c }{\frac{1}{3^{2}}-\frac{1}{4^{2}}}=\frac{144 c }{7}( n =4\) to \(n =3)\)
\(\Delta \lambda=\lambda_{2}-\lambda_{1}=\frac{144 c }{7}-9 c =\frac{81 c }{7}=\frac{81 \times 912}{7}\)
\(=10553.14 \mathring {A}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
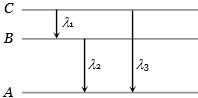
- 1ચોક્કસ અણુના $A, B, C$ ઉર્જા સ્તરો માટે વધતી ઊર્જાના મૂલ્યો ${E_A} < {E_B} < {E_C}$ છે. જો ${\lambda _1},\;{\lambda _2},\;{\lambda _3}$ અનુક્રમે $C$ થી $B, \;B$ થી $A$ અને $C$ થી $A$ સંક્રાતિ દરમિયાન ઉત્સર્જન થતી તરંગલંબાઇ હોય, તો કયું વિધાન સાચું થાય?View Solution
- 2ક્ષ-કિરણની તરંગલંબાઈ $10 \, \mathring A$ છે. ક્ષ-કિરણ ફોટોન જેટલી ઉર્જા ધરાવતા એક કાલ્પનિક કણનું દળ $\frac{ x }{3} h \,kg$ હોય તો $x$ નું મૂલ્ય કેટલું હશે? $(h =$ પ્લાંકનો અચળાંક$)$View Solution
- 3જો હાઇડ્રોજન વર્ણપટના પારજાંબલી વિભાગની સૌથી લાંબી તરંગલંબાઇ ${\lambda _0}$ છે, તો તેના પારરકત વિભાગની ન્યુનત્તમ તરંગલંબાઇ કેટલી થાય?View Solution
- 4કાર્બનમાંથી $22\, pm$ તરંગલંબાઈનાં ક્ષ કિરણો આપાત કિરણ પૂંજ સાથે $85^{\circ}$ના ખૂણે પ્રકિર્ણન પામે છે. ક્ષ કિરણો માટે કોમ્પ્ટોન સ્થાનાંતર ......... $pm$ છે ? $\left(\cos 85^{\circ}=0.088\right)$View Solution
- 5હાઇડ્રોજનની ધરા-સ્થિતિમાં રહેલા ઇલેકટ્રોનની આયનીકરણ ઊર્જા $13.6 \;eV$ છે. હાઇડ્રોજનમાં ધરા-સ્થિતિમાં રહેલ ઇલેકટ્રોનને $12.1\; eV $ ઊર્જા ધરાવતા ફોટોન વડે ઉત્તેજિત કરવામાં આવે છે. બોહરની થીયરી પ્રમાણે હાઇડ્રોજન દ્વારા ઉત્સર્જન થતી વર્ણપટ રેખાની સંખ્યા કેટલી હશે?View Solution
- 6હાઇડ્રોજન પરમાણુ માટે $3$$ \to $$2 $ સંક્રાંતિને અનુરૂપ વિકિરણ ધાતુ સપાટી પર પડતા ફોટોઇલેકટ્રોન ઉત્પન્ન કરે છે.આ ઇલેકટ્રોનને $3 \times 10^{-4}$ $T$ વાળા ચુંબકીયક્ષેત્રમાં દાખલ કરવામાં આવે છે.જો ઇલેકટ્રોનનાં સોૈથી મોટો વર્તુળામાર્ગની ત્રિજયા $10.0$ $mm$ હોય,તો ધાતુનું વર્ક ફંકશન _____$ eV$ ને નજીક થશે.View Solution
- 7View Solutionક્ષ-કિરણોનું વંકન થતું નથી કારણ કે .....
- 8સૂચી $I$ અને સૂચી $II$ મેળવો.View Solution
સૂચી$I$(હાઈડ્રોજનમાટેવર્ણપટરેખાઓસંકાંતિમાંથી) સૂચી$11$(તરંગલંબાઈ ($nm$) $A$ $n_2=3 $ થી $n_1=2$ $I$ $410.2$ $B$ $n_2=4$ થી $n_1=2$ $II$ $434.1$ $C$ $n_2=5$ થી $n_1=2$ $III$ $656.3$ $D$ $n_2=6$ થી $n_1=2$ $IV$ $486.1$ નીચે આપેલા વિક્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 9View Solutionહાઈડ્રોજન પરમાણુ ના બોહર મોડેલ માં સાચું વિધાન કયું છે.
- 10હાઇડ્રોજન $(_1H^1),$ડયુટેરિયમ $(_1H^2)$,એક આયનિત હિલિયમ $(_2He^4)^+$ અને દ્વિઆયનિત લિથિયમ ${\left( {{}_3^6Li} \right)^{ + + }}$, ને નાભી ( ન્યુકિલયસની ની ફરતે એક ઇલેકટ્રોન હોય છે.ઇલેકટ્રોનની સંક્રાંતિ $n=2$ થી $ n=1 $ લો. જો ઉત્પન્ન થતા વિકિરણની તરંગલંબાઇ અનુક્રમે $λ_1,λ_2,λ_3$ અને $λ_4$ હોય,તો નીચેનામાંથી કયું વિધાન સાચા વિધાનને સંનિકટ છે?View Solution
