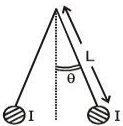
Let us consider \('l'\) length of current carrying wire.
At equilibrium
\(\mathrm{T} \cos \theta=\lambda \mathrm{g} \ell\)
and \(T \sin \theta=\frac{\mu_{0}}{2 \pi} \frac{I \times I l}{2 L \sin \theta}\left[\because \frac{F_{B}}{\ell}=\frac{\mu_{0}}{4 \pi} \frac{2 I \times I}{2 \ell \sin \theta}\right]\)
Therefore, \(I=2 \sin \theta \sqrt{\frac{\pi \lambda g L}{u_{0} \cos \theta}}\)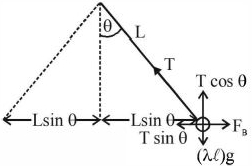
Download our appand get started for free
Similar Questions
- 1$100 \;\Omega$ અવરોધ ધરાવતું ગેલ્વેનોમીટર એ $10\; mA$ વિદ્યુતપ્રવાહ પર પૂર્ણ સ્કેલ આવર્તન આવે છે. તો શંટનું મુલ્ય કેટલો હોવો જોઈએ કે જેથી તે $100 \;mA$ વિદ્યુતપ્રવાહ માપી શકે?View Solution
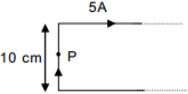
- 2$P$ પાસે એકમ લંબાઈ દીઠ બળ શોધો.View Solution
- 3$m$ દળ અને $Q$ વિદ્યુતભાર અને $K$ ગતિઊર્જા ધરાવતો કણ એકસમાન ચુંબકીયક્ષેત્રમાં લંબરૂપે દાખલ થાય છે.તો $ 3 \,sec $ પછી ગતિઊર્જા......$K$ થાય.View Solution
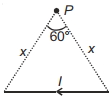
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે $I$ વિદ્યુતપ્રવાહ ધરાવતો સિમિત સીધો તાર બિંદુ $P$ પાસે $60^{\circ}$ ખૂણો બનાવે છે. $P$ પાસે ચુંબકીય ક્ષેત્ર કેટલું છે ?View Solution
- 5બે એકસસમાન વાહકતારો $AOB$ અને $COD$ ને પરસ્પર લંબ મૂકેલા છે. $AOB$ માંથી $I _{1}$ તથા $COD$ માંથી $I _{2}$ વિદ્યુતપ્રવાહ પસાર થાય છે. આ વાહકતારો $AOB$ અને $COD$ ના સમતલને લંબ એવી દિશામાં, $O$ થી $d$ અંતરે આવેલા બિંદુએ યુંબકીય ક્ષેત્રનું મૂલ્ય કેટલું હશે?View Solution
- 6એક ઈલેકટ્રોનને અયળ વેગ સાથે સુરેખ સોલેનોઈડ વીજપ્રવાહ ધારીત અક્ષ પર ગતિ કરે છે.View Solution
$A$. ઈલેકટ્રોન સોલેનોઈડ અક્ષ પર ચુંબકીય ક્ષેત્ર અનુભવશે.
$B$. ઈલેકટ્રોન ચુંબકીય બળ અનુભવતો નથી .
$C$. ઈલેકટ્રોન સોલેનાઈડ અક્ષ પર ગતિ કરે છે.
$D$. ઈલેકટ્રોન સોલેનાઈડની અક્ષ પર પ્રવેગિત થાય છે.
$E$. ઈલેકટ્રોન સોલેનાઈડની અંદરની બાજુએ પરવલય માર્ગને અનુસરે છે.
નીચેના વિકલ્પોમાંથી યોગ્ય વિકલ્પ પસંદ કરો.
- 7$r$ ત્રિજ્યા ધરાવતી અને $I$ પ્રવાહધારીત રીંગનાં કેન્દ્રથી $R$ અંતરે ચુંબકીયક્ષેત્ર કેટલું થશે?View Solution
- 8View Solutionકોપરનો બનેલા લાંબા પોલા નળાકારમાંથી વિદ્યુતપ્રવાહ પસાર કરતાં તેમાંથી ઉત્પન્ન થતું ચુંબકીયક્ષેત્ર ...
- 9$f $ આવૃત્તિવાળું વિદ્યુતક્ષેત્ર $R$ ત્રિજયાની સાઇકલોટ્રોનની ડીશ પર લગાવવામાં આવે છે.સાઇકલોટ્રોનમાં ચુંબકીયક્ષેત્ર $B$ અને પ્રોટ્રોનની ગતિઊર્જા $K$View Solution
પ્રોટોનને(દળ = $m$) પ્રવેગિત કરવા સાયક્લોટ્રોનની ડિસ (ત્રિજ્યા $R$) ની વચ્ચે $f$ આવૃતિ ધરાવતું પ્રત્યાવર્તી વિદ્યુતક્ષેત્ર લગાવવામાં આવે છે. સાયક્લોટ્રોનમાં વપરાતું ચુંબકીય ક્ષેત્ર $(B)$ અને પ્રોટોન બીમના કારણે ઉત્પન્ન થતી ગતિઊર્જા $(K)$ શેના વડે આપી શકાય?
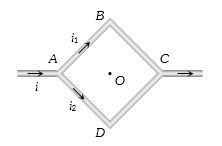
- 10ચોરસ $ABCD$ ની બાજુની લંબાઇ $a$ છે, $ABC$ અને $ADC$ નો અવરોધ અનુક્રમે $r$ અને $2r$ છે,તો કેન્દ્ર પર ચુંબકીય ક્ષેત્ર કેટલું થાય?View Solution