$F{e^2}+ \left( {aq} \right) + A{g^ + }\left( {aq} \right) \to F{e^{3 + }}\left( {aq} \right) + Ag\left( s \right)$
$E_{Ag^+/Ag}^o = xV$, $E_{F{e^{2 + }}/Fe}^o = yV$, $E_{F{e^{3 + }}/Fe}^o = zV$
\(F{{e}^{2+}}(aq)\,+\,A{{g}^{+}}(aq)\,\to \,F{{e}^{3+}}\,(aq)\,+\,Ag\,(s)\)
\(E_{cell}^o\, = \,3\)
Given :
\(E_{A{g^ + }/Ag}^o\, = \,x\) ....... \((1)\)
\(E_{F{e^{2 + }}/Fe}^o\, = \,y\) ....... \((2)\)
\(E_{F{e^{3 + }}/Fe}^o\, = \,Z\) ....... \((3)\)
Using equation:
\(\Delta {G^o}\, = \, - \,nF{E^o}\)
\(\Delta G_1^0\, = \, - \,Fx\)
\(\Delta G_2^0\, = \, - \,2Fy\)
\(\Delta G_3^0\, = \, - \,3Fz\)
\(F{e^{2 + }}\, + \,2{e^ - }\, \to \,Fe\, - \,2Fy\)
\(\mathop {F{e^{3 + }}}\limits_ - \, + \,\mathop {3{e^ - }}\limits_ - \, \to \,\mathop {Fe}\limits_ - \, - \,\mathop {3Fz}\limits_ + \)
\(\overline {F{e^{2 + }}\, \to \,F{e^{3 + }}\, + \,{e^ - }\,( - 2Fy\, + \,3Fz)} \)
\(\underline {A{g^ + }\, + \,{e^ - }\, \to \,Ag\, - \,Fx} \)
\(\Delta {G_{Total\,}}\, = \, - \,2\,Fy\, + \,3Fz\, - \,Fx\, = \, - \,FE_{cell}^o\)
\(E_{cell}^o\, = \,x\, + \,2y\, - \,3z\)
Download our appand get started for free
Similar Questions
- 1આપેલા કોષ નો કોષ અચળાક $0.47\,cm^{-1}$ આ કોષમાં મુકેલા દ્રાવણનો પ્રતિકાર $31.6$ ઓહમ માપવામાં આવે છે.તો દ્રાવણ ની વાહકતા શું હશે ?View Solution
- 2$Zn, Cu, Ag, H_2$ અને $Ni$ ના ઓક્સિડેશન પોટેન્શિયલ અનુક્રમે $0.76, -0.34, -0.80, 0,0.55$ છે. કઈ પ્રક્રિયા મહત્તમ વોલ્ટેજ પુરો પાડે છે?View Solution
- 3$298\,K$ પર નીચે આપેલા કોષનો કોષ પોટેન્શિયલ $X \left| X ^{2+}(0.001 M ) \| Y ^{2+}(0.01 M )\right| Y$ એ $..............\times 10^{-2}\,v$ છે.View Solution
આપેલ: $E _{ x ^{2+} \mid x }^0=-2.36\,V$
$E _{ Y ^{3+} \mid Y }^0=+0.36\,V$
$\frac{2.303\,RT }{ F }=0.06\,V$
- 4$Ba^{2+}$ અને $Cl^{-}$ ની અનંત મંદને આયનીય વાહકતા અનુક્રમે $127$ અને $76 $ ઓહમ$^{-1}$ સેમી$^{-1}$ તુલ્ય$^{-1}$ છે, તો અનંત મંદને $BaCl_2 $ની તુલ્યવાહકતા ..... થાય.View Solution
- 5$KCl,\,NaCl$ અને $KNO_3$ ની મોલર વાહકતા અનુક્રમે $152,\,128$ અને $111\, S\, cm^{2}\, mol^{-1}$ છે, તો $NaNO_3$ ની મોલર વાહકતા ............. ${\rm{S}}\,{\rm{c}}{{\rm{m}}^2}{\rm{mo}}{{\rm{l}}^{ - 1}}$ થાય.View Solution
- 6જુદા-જુદા પ્રકારના અર્ધ કોષોનો $\left(\frac{\partial E }{\partial T }\right)_{ P }$ નીચે મુજબ છે.View Solution
$\text { A } \quad\quad\quad\quad\quad \text { B } \quad\quad\quad\text { C } \quad\quad\quad\quad\text { D }$
$1 \times 10^{-4} \quad 2 \times 10^{-4} \quad 0.1 \times 10^{-4} \quad 0.2 \times 10^{-4}$
(અહિયાં,$E$ એ ઇલેક્ટ્રોમોટીવ બળ છે.)
ઉપર આપેલા અર્ધકોષો માંથી ક્યાનો સંદર્ભ ઈલેક્ટ્રોડ તરીકેનો ઉપયોગ પસંદગીય પામશે ?
- 7આપેલ $E_{C{u^{2 + }}/Cu}^o = 0.34\,V\,,\,E_{C{u^{2 + }}/Cu}^o = 0.15\,V$ તો $Cu^+/Cu$ અર્ધકોષ માટે પ્રમાણિત વિર્ધુતધ્રુવ પોટેન્શિયલ ............. $\mathrm{V}$View Solution
- 8$Z{n^{2 + }}/Zn$ ની ઇલેક્ટ્રોડ પોટેન્શિયલ $ - 0.76\,V$ અને $C{u^{2 + }}/Cu$ માટે મૂલ્ય $ + 0.34V$ છે.આ બંને ઇલેક્ટ્રોડોની વચ્ચે બનાવેલ કોષનો $EMF$ ...... $\mathrm{V}$ છે.View Solution
- 9$E _{ Cu ^{2+} \mid Cu }^{\circ}=+0.34 V$View Solution
$E _{ Zn ^{2}+\mid Zn }^{ o }=-0.76 V$
ઉપરોક્ત કોષ માટે નીચેના વિકલ્પોમાંથી ખોટા વિધાનની ઓળખ આપો
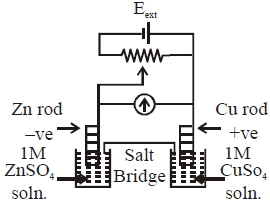
- 10$KN{O_3}$ના સંતૃપ્ત દ્રાવણનો ઉપયોગ ‘ક્ષાર સેતુ ’ બનાવવા માટે થાય છે કારણ કેView Solution
