Let \(B_H\) and \(B_v\) be the horizontal and vertical components of earth's magnetic field \(\vec B\). Since \(\theta\) is the angle of dip
\(\tan \theta = \frac{B_V}{B_H}\)
or \(cot\theta = \frac{B_H}{B_V}\)
Suppose planes \(1\) and \(2\) are two mutually perpendicular planes and respectively make angles \(\theta\) and \(90°- \theta\) with the magnetic meridian. The vertical components of earth's magnetic field remain same in the two planes but the effective horizontal components in the planes will be
\(B_{1}=B_{H} \cos \theta \text { and } B_{2}=B_{H} \sin \theta\)
The angles of \(\operatorname{dip} \theta_{1}\) and \(\theta_{2}\) in the two planes are given by
\(\tan \theta_{1}=\frac{B_{V}}{B_{1}}\)
\(\tan \theta_{1}=\frac{B_{V}}{B_{H} \cos \theta}\)
or \(\quad \cot \theta_{1}=\frac{B_{H} \sin \theta}{B_{V}}.........(ii)\)
\(\text { Similarly, } \cot \theta_{2}=\frac{B_{H} \sin \theta}{B_{V}}.........(iii)\)
From eqns. \((ii)\) and \((iii)\)
\(\cot ^{2} \theta_{1}+\cot ^{2} \theta_{2}=\frac{B_{H}^{2}}{B_{V}^{2}}\left(\cos ^{2} \theta+\sin ^{2} \theta\right)=\frac{B_{H}^{2}}{B_{V}^{2}}\)
\(\therefore \quad \cot ^{2} \theta_{1}+\cot ^{2} \theta_{2}=\cot ^{2} \theta \quad[\text { from eqn. (i) }]\)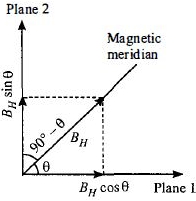
Download our appand get started for free
Similar Questions
- 1View Solutionઅણુની ચુંબકીય મોમેન્ટ કયાં પદાર્થમાં શૂન્ય ન હોય?
- 2સમાન દળ,લંબાઇ અને પહોળાઇ ધરાવતા બે ચુંબકોની ચુંબકીય મોમેન્ટ $M $ અને $2M$ છે.તેમને સમાન ધ્રુવો ભેગા રાખીને બાંધીને દોલનો કરાવતાં તેનો આવર્તકાળ $3 \,sec$ મળે છે. તો અસમાન ધ્રુવો ભેગા રાખીને દોલનો કરાવતાં તેનો આવર્તકાળ કેટલો થાય?View Solution
- 3એકબીજાને લંબ રાખીને બે સમાન ગજિયા ચુંબકને દોલનો કરાવતાં આવર્તકાળ $ {2^{5/4}} \,sec$ મળે છે.જો એક ચુંબકને દૂર કરવામાં આવે,તો નવો આવર્તકાળ કેટલો થાય?View Solution
- 4નીચે બે કથન આપેલ છે.View Solution
કથન $I$: ડાયા મેગ્નેટિક પદાર્થ માટે $-1 \leq \chi < 0$, જ્યાં $\chi$ એ ચુંબકીય સસેપ્ટીબીલીટી છે.
કથન $II$: ડાયા મેગ્નેટિક પદાર્થને જ્યારે બાહ્ય ચુંબકીય ક્ષેત્રમાં મૂકવામાં આવે છે ત્યારે તે ક્ષેત્રના પ્રબળ ભાગમાંથી નિર્બળ ભાગ તરફ ગતિ કરવાનું વલણ ધરાવ છે.
ઉપર્યુક્ત બંને કથનોના સંદર્ભમાં, નીચે આપેલ વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 5ગજિયા ચુંબકને ચુંબકીયક્ષેત્રમાં શિરોલંબ રાખેલ છે.તેના પર લાગતું ટોર્ક અડધું કરવા માટે તેને કેટલા .....$^o$ ફેરવવો પડે?View Solution
- 6View Solutionપૃથ્વીના ચુંબકીયક્ષેત્રને સમક્ષિતિજ ધટક શૂન્ય કયાં સ્થાન આગળ થાય?
- 7સાલિયાના પદાર્થની મેગ્નેટિક સસેપ્ટિબિલિટી $499$ છે. શૂન્યાવકાશની પરમિએબિલિટી $4 \pi \times 10^{-7}\;{H} / {m}$ છે. સાલિયાના પદાર્થની નિરપેક્ષ પરમિએબિલિટી $....\,\pi \times 10^{-4} {H} / {m}$ હશે.View Solution
- 8View Solutionવિદ્યુતચુંબકોના દ્રવ્યમાં નરમ લોખંડના વપરાશ કરવાના બે કારણો
- 9$10^{-3}\, m ^{3}$ કદ અને $1000$ સાપેક્ષ પરમિએબિલિટી ધરાવતા લોખંડના સળિયાને $10$ આટા/$cm$ ધરાવતા સોલેનોઇડ માં મૂકીને $0.5\,A$ પ્રવાહ પસાર કરતા ઉદ્ભવતી મેગ્નેટિક મોમેન્ટ $...........Am^2$View Solution
- 10એક સ્થળે પૃથ્વીના ચુંબકીયક્ષેત્રનો સમક્ષિતિજ ઘટક $ {B_0} $ અને શિરોલંબ ઘટક $ {V_0} $ સમાન હોય,તો ત્યાં પૃથ્વીનું ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
