સંકોચાયા બદનુકદ \({\upsilon _2} = \frac{1}{{64}}{\upsilon _1}\,\,\,(\) જ્યાં \({\upsilon _{\text{1}}}{\text{ = }}\) પૃથ્વી નું હાલનુ કદ )
\(\therefore \frac{4}{3}\pi {R_2}^3 = \frac{1}{{64}} \times \frac{4}{3}\,\pi {R_1}^3\,\,\,\,{\text{(}}\) જ્યાં \({{\text{R}}_{\text{1}}}{\text{ = }}\)પૃથ્વીની હાલ ની ત્રિજ્યા \(,{\text{ }}{{\text{R}}_{\text{2}}}\) પૃથ્વી ની નવી ત્રિજ્યા )
\(\therefore \,{R_2} = \frac{1}{4}{R_1}\) પૃથ્વી પર બાહ્ય તોર્ક લાગતો ના હોવાથી
\(\,L = I\omega = I\left( {\frac{{2\pi }}{T}} \right) = \,\) અચળ \(\,\,\therefore \,{I_1}\left( {\frac{{2\pi }}{{{T_1}}}} \right) = {I_2}\,\,\left( {\frac{{2\pi }}{{{T_2}}}} \right)\)
\(\therefore \,\left( {\frac{2}{5}M{R_1}^2} \right) \times \frac{1}{{{T_1}}} = \left( {\frac{2}{5}M{R_2}^2} \right) \times \frac{1}{{{T_2}}}\,\)
\(\therefore {T_2} = \left( {\frac{{{R_2}}}{{{R_1}}}} \right) \times {T_1}\)
\(\therefore \,{T_2} = \left( {\frac{{\frac{{{R_1}}}{4}}}{{{R_1}}}} \right)\, \times {T_1}\,\,\,\left( {\because {R_2} = \frac{1}{4}{R_1}} \right)\, = {\left( {\frac{1}{4}} \right)^2} \times 24\,\)
\(\,(\because {T_1} = 24\,h)\,\, = \frac{1}{{16}} \times 24 = 1.5\,\,h\)
Download our appand get started for free
Similar Questions
- 1$M$ દળ ધરાવતી ગબડતી રીંગની ઝડપ $V$ થી $3\ V$ થાય,તો તેની ગતિઊર્જામાં થતો ફેરફારView Solution
- 2એક સંતુલન ત્રાજવું અસમાન લંબાઈના હાથ ધરાવે છે. જો પદાર્થ ને એક તવી (ત્રાજવાનું પાન) માં રાખતા વજન $18 \,kg$ થાય અને બીજી તવીમાં રાખતા વજન $8 \,kg$ થાય તો પદાર્થનું સાચું વજન ........ $kg$ થાય.View Solution
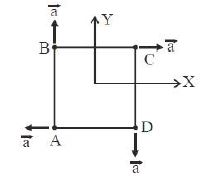
- 3ચોરસના ચાર બિંદુ પર ચાર કણ $A, B, C$ અને $D$ જેના દળ $m_A=m, m_B=2m, m_C=3m$ અને $m_D=4m$ મૂકેલા છે.આકૃતિમાં દર્શાવ્યા પ્રમાણેની સમાન મૂલ્યના પ્રવેગથી ગતિ કરે તો તેના દ્રવ્યમાન કેન્દ્રનો પ્રવેગ કેટલો થાય?View Solution
- 4$1\ kg $ અને $3\ kg$ આંતરિક બળોના કારણે એકબીજા તરફ ગતિ કરે છે.જયારે તેમનો સાપેક્ષ વેગ $2\ m/s$ હોય,ત્યારે દ્રવ્યમાન કેન્દ્ર નો વેગ $0.5\ m/s$ છે.તો જયારે તેમનો સાપેક્ષ વેગ $3\ m/s$ હોય,ત્યારે દ્રવ્યમાન કેન્દ્ર નો વેગ ......... $m/s$ થાય.View Solution
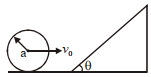
- 5$‘a'$ ત્રિજ્યા અને $'m’$ દળ ધરાવતો ગોળો, અચળ ગતિ $v_{0}$ સાથે સમક્ષિતીજ સમતલને સમાંતર ગબડે છે. આ દરમ્યાન તે સમક્ષિતીજ સાથે $\theta$ કોણે નમેલા સમતલ સામનો કરતાં તેના ઉપર ચઢે છે. જો આપણે ધારી લઈએ કે તે લપસ્યા વગર ગબડે છે તો આ ગોળો ઉપરની દિશામાં કેટલું અંતર કાપશે?View Solution
- 6એક લાંબા સમક્ષિતિજ સળિયા પર તેની લંબાઈને અનુરૂપ ગતિ કરતો મણકો રાખેલો છે, પ્રારંભમાં મણકાને સળિયાના એક છેડા $A$ થી $L$ અંતરે રાખેલો છે. સળિયાને છેડા $A$ ની ફરતે અચળ કોણીય પ્રવેગ $\alpha$ થી કોણીય ગતિ કરવવામાં આવે છે. જો સળિયા અને મણકા વચ્ચેનો ઘર્ષણાંક $\mu$ હોય અને ગુરુત્વાકર્ષણ ને અવગણીએ તો મણકો કેટલા સમય પછી સળિયા પર દડશે?View Solution
- 7કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ તેવી અક્ષને અનુલક્ષીને એક પાતળી નિયમિત તકતીની ચક્રાવર્તન ત્રિજ્યા અને તકતીના વ્યાસને ફરતે ચક્રાવર્તન ત્રિજ્યાનો ગુણોતર $......$ હશે.View Solution
- 8$3\ kg$ દળના દઢ પદાર્થને $ 2\ kg$ સાથે દળ રહિત સળિયા સાથે જોડેલો છે. $3\ kg$ દાળ ${{{\vec r}}_{\,{\text{1}}}}\, = \,\,(2\,\hat i\,\, + \,\,5\,\hat j)\,m$ પર અને ${\text{2}}\,{\text{kg}}$ દળ ${{{\vec r}}_{\,{\text{2}}}}\, = \,\,(4\,\hat i\,\, + \,\,2\,\hat j)\,m$ દળ પર રહેલા છે. સળિયાની લંબાઈ અને દ્રવ્યમાન કેન્દ્રના યામ શોધો.View Solution
- 9View Solutionકેન્દ્રગામી બળના કારણે ચાકગતિ કરતા કાણનું કોણીય વેગમાન અચળ નીચેના પૈકી ક્યા કારણે હોય છે?
- 10$m$ દળનો એક કણ એ વેગ $v$ થી સમક્ષિતિજ સાથે $30^{\circ}$ નો ખૂણો બનાવીને પ્રક્ષિપ્ત ગતિ કરે છે. આ કણ જ્યારે મહત્તમ ઉંચાઈ પ્રાપ્ત કરે તે સમયે, ગતિની શરૂઆતના બિંદુની સાપેક્ષે કણના કોણીય વેગમાનનું મૂલ્ય ફેટલું હશે?View Solution
