\(E\,\, = \,{G^p}{h^q}{C^r}\,\)
\(\left[ {{M^1}{L^2}{T^{ - 2}}} \right]\,\, = \,\,{\left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]^p}{\left[ {{M^1}{L^2}{T^{ - 1}}} \right]^q}\,\,{\left[ {{L^1}{T^{ - 1}}} \right]^r}\)
\(m\) નો પાવર \( \Rightarrow \,\,1\, = - p\,\, + \;\;q\,\, + \;\,0\,\,\,........\left( i \right)\)
\(L\) નો પાવર \(\, \Rightarrow \,\,2\,\, = \,\,3p\,\, + \,\,2q\,\, + \,\,r\,\,...........\left( {ii} \right)\)
\(T\) નો પાવર \( \Rightarrow - 2\,\, = - 2P\,\, - \,\,q\,\, - \,\,r\,\,\,\,.............\left( {iii} \right)\)
આ સમીકરણ ને ઉકેલવા \(\,\,p\,\, = \,\, - \frac{1}{2},\,\,q\,\, = \,\,\frac{1}{2}\,\,r\,\, = \,\,\frac{5}{2}\)
Download our appand get started for free
Similar Questions
- 1View Solutionવિકૃતિનું પારિમાણિક સૂત્ર શું થાય?
- 2કોઈ ભૌતિક રાશિ $p$ ને $p\, = a^{1/2}\, b^2\, c^3\, d^{-4}$ થી દર્શાવેલ છે. જો $a, b, c$ અને $d$ ના માપનમાં રહેલી સાપેક્ષ ત્રુટિ અનુક્રમે $2\% , 1\%, 3\%$ અને $5\%$ હોય, તો $P$ માં રહેલી સાપેક્ષ ત્રુટિ $........... \%$ હશે.View Solution
- 3જો $C$ કેપેસીટન્સ ધરાવતા કેપેસીટરની બે પ્લેટ વચ્ચેનો વિદ્યુતસ્થિમાનનો તફાવત $V$ વડે દર્શાવવામાં આવે તો $C{V^2}$ નું પારિમાણિક સૂત્ર શું થાય?View Solution
- 4અવરોધ ધરાવતા માધ્યમમાં સ્થિર સ્થિતિમાંથી નીચે પડતાં પદાર્થના વેગમાં થતો ફેરફાર $\frac{{dV}}{{dt}} = At - BV$ મુજબ આપવામાં આવે છે . તો $A$ અને $B$ નું પારિમાણિક સૂત્ર શું થાય?View Solution
- 5$P = \frac{{a - {t^2}}}{{bx}}$ છે જ્યાં $P$ દબાણ, $x$ અંતર અને $t$ સમય છે તો $a/b$ નું પરિમાણિક સૂત્ર શું થાય?View Solution
- 6View Solutionપ્રતિબળનું પરિમાણ ................. છે
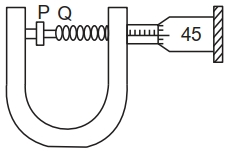
- 7સ્ક્રુગેજની મદદથી તારનો વ્યાસ માપવાના એક પ્રયોગમાં નીચે મુજબના અવલોકનો મળે છે.View Solution
$(A)$ એક પૂર્ણ પરિભ્રમણ માટે સ્ક્રુ મુખ્ય સ્કેલ ઉપર $0.5\,mm$ ખસે છે.
$(B)$ વર્તુળાકાર સ્કેલ પર કુલ $50$ કાપા છે.
$(C)$ મુખ્ય સ્કેલ પરનું અવલોકન $2.5\,mm$ છે.
$(D)$ વર્તુળાકાર સ્કેલ પરનો $45$ મો કાપો પીચ-રેખા પર આવે છે.
$(E)$ સાધનને $0.03\,mm$ જેટલી ઋણ ત્રુટી છે.
તો તારનો વ્યાસ $............\;mm$ થશે.
- 8એક લાક્ષણિક દહનશીલ એન્જીન (કંબશન એન્જીન) માં વાયુનાં અણુ દ્વારા થયેલ કાર્યને $W=\alpha^{2} \beta e^{\frac{-\beta x^{2}}{k T}}$ દ્વારા આપવામાં આવે છે જ્યાં $x$ સ્થાનાંતર, $k$ બોલ્ટ્ઝમેન અચળાંક અને $T$ તાપમાન દર્શાવે છે. જો $\alpha$ અને $\beta$ અચળાંકો હોય, તો $\beta$ નું પરિમાણ ......... હશે.View Solution
- 9જો ટ્રાવેલિંગ માઇક્રોસ્કોપના મુખ્ય સ્કેલ પરના $49$ કાપાઓ વર્નિયર ડિવિઝન (વિભાગ)ના $50$ કાપાઓ બરાબર હોય અને મુખ્ય સ્કેલ પરનું નાનામાં નાનું અવલોકન $0.5 \mathrm{~mm}$ હોય, તો . ટ્રાવેલિંગ માઈક્રોસ્કોપ માટેનો વર્નિયર અચળાંક________છે.View Solution
- 10View Solutionલંબાઈ શેમાં માપી શકાય નહીં?
