જ્યારે $m$ દળનાં પદાર્થને પૃથ્વીની સપાટી થી $n R$ ઊંચાઈ એ લઈ જવામાં આવે તો સ્થિતિ ઉર્જામાં થતો ફેરફાર શું હશે ? ($R$ પૃથ્વીની ત્રિજ્યા)
Medium
Download our app for free and get started
c
(c)
(c)
Potential energy at the surface \(=-\frac{G M m}{R}\)
Potential energy at height, \(n R=-\frac{G M m}{(n+1) R}\)
Change in potential energy \(=-\frac{G M m}{(n+1) R}+\frac{G M m}{R}\)
\(=\frac{G M m}{R}\left(\frac{-1+n+1}{n+1}\right)\)
\(=\left(\frac{n}{n+1}\right)\left(\frac{G M}{R^2}\right) m \times R\)
\(=m g R\left(\frac{n}{n+1}\right)\)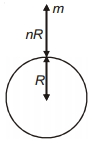
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પદાર્થને $2R$ ત્રિજ્યાની ભ્રમણકક્ષા થી $3R$ ત્રિજ્યાની ભ્રમણકક્ષા માં લઈ જવા માટે કેટલુ કાર્ય કરવું પડે?View Solution
- 2$m_1$ અને $m_2$ દળ ધરાવતા બે પદાર્થ શરૂઆતમાં અનંત અંતરે છે.તે બંને એકબીજા તરફ ગુરુત્વાકર્ષણને કારણે ગતિ કરે છે.જ્યારે તે એકબીજાથી $r$ અંતરે હોય ત્યારે તેનો સાપેક્ષ વેગ કેટલો હશે?View Solution
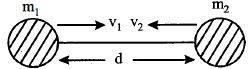
- 3બે કાલ્પનિક $m_1$ અને $m_2$ દળ ધરાવતા ગ્રહ એક બીજાથી અનંત અંતરે છે.હવે ગુરુત્વાકર્ષણને કારણે તેમના કેન્દ્રને જોડતી રેખા પર તે એકબીજા તરફ ગતિ કરે છે.જ્યારે તેમની વચ્ચેનું અંતર $d$ હોય ત્યારે તેમની ઝડપ કેટલી હશે? $(m_1$ ની ઝડપ $v_1$ અને $m_2$ ની ઝડપ $v_2$ છે $)$View Solution
- 4View Solutionએક સ્પ્રિંગ બેલેન્સ દરિયાની સપાટી પર આખેલું છે. હવે જો હવે તેને પૃથ્વીની સપાટીથી ઊંચાઈ પર લઈ જવામાં આવે તો સ્પ્રિંગ બેલેન્સ નું વજન...
- 5મંગળ ગ્રહ પાસે બે ચંદ્ર છે. જો એકનો આવર્તકાળ $7\, hours,\, 30\, minutes$ અને કક્ષાની ત્રિજયા $9.0 \times 10^{3}\, {km}$ હોય તો મંગળ ગ્રહનું દળ કેટલું હશે?View Solution
$\left\{\frac{4 \pi^{2}}{G}=6 \times 10^{11} {N}^{-1} {m}^{-2} {kg}^{2}\right\}$
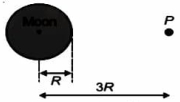
- 6જો $R$ ત્રિજ્યા અને $M$ દળનાં ચંદ્રના કેન્દ્રથી $3 R$ અંતર $P$ બિંદુથી સ્થિર પદાર્થને મૂક્ત કરવામાં આવે છે. નીચે આપેલી કઈ ઝડપે પદાર્થને ચંદ્રને અથડાશે ?View Solution
- 7ચંદ્રને પૃથ્વી ફરતે $1$ પરિભ્રમણ પૂર્ણ કરતાં $29$ દિવસ લાગે છે .જો ચંદ્રનું દળ બમણું કરવામાં આવે પણ બીજા બધા પરિમાણ પહેલા જેટલા રાખવામા આવે તો 1 પરિભ્રમણ પૂર્ણ કરતાં લાગતો સમય ....... $(day)$ થાય ?View Solution
- 8ચંદ્ર અને પૃથ્વીના કેન્દ્ર વચ્ચેનું અંતર $D$ છે.જો પૃથ્વીનું દળ ચંદ્ર કરતાં $81$ ગણું હોય,તો પૃથ્વીના કેન્દ્રથી કેટલા અંતરે ગુરુત્વાકર્ષણ બળ શૂન્ય થાયView Solution
- 9View Solutionસૂર્યની ફરતે ભ્રમણ કરતાં ગ્રહ માટે નીચેના માથી ક્યો ગ્રાફ સાચો છે ?
- 10$M $ દળ ના બે ટુકડા $xM$ અને $(1-x)M$ કરવામાં આવે છે.તો $x$ ની કઇ કિંમત માટે તેમની વચ્ચે લાગતું ગુરુત્વાકર્ષણ બળ આપેલા અંતર માટે મહત્તમ થાય?View Solution