\(x={A} \sin \omega {t}+{B} \sin \omega {t}\)
\({v} ={A} \sin \omega {t}+{Bcos} \omega {t}\)
\({{dt}}={A} \omega \cos \omega {t}-{B} \omega \sin \omega {t}\)
\({At} {t}=0, {x}(0)={B}\)
\({v}(0)={A} \omega\)
\({x}={A} \sin \omega {t}+{B} \sin \left(\omega {t}+90^{\circ}\right)\)
\(A_{\text {net }}=\sqrt{A^{2}+B^{2}}\)
\(\tan \alpha=\frac{B}{A} \Rightarrow \cot \alpha=\frac{A}{B}\)
\(\Rightarrow \quad x=\sqrt{A^{2}+B^{2}} \sin (\omega t+\alpha)\)
\(\Rightarrow \quad x=\sqrt{A^{2}+B^{2}} \cos (\omega t-(90-\alpha))\)
\(x=C \cos (\omega t-\phi)\)
\(\Rightarrow C=\sqrt{A^{2}+B^{2}}\)
\(C= \sqrt{\frac{[v(0)]^{2}}{\omega^{2}}+[x(0)]^{2}}\)
\(\phi= 90-\alpha\)
\(\tan \alpha=\cos \alpha=\frac{A}{B}\)
\(\Rightarrow \tan \phi=\frac{v(0)}{x(0) \cdot \omega}\)
\(\phi= \tan ^{-1}\left(\frac{v(0)}{x(0) \omega}\right)\)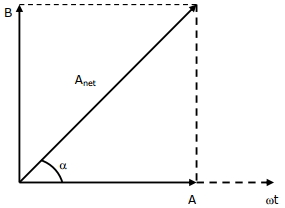
Download our appand get started for free
Similar Questions
- 1View Solutionસરળ આવર્તગતિ માટે ખોટું વિધાન પસંદ કરો.
- 2સમીકરણ $4 \frac{d^2 x}{d t^2}+320 x=0$ અનુસાર એક કણ સરળ આવર્તગતિ કરે છે. તેનાં કંપનનો આવર્તકાળ કેટલો હેશે ?View Solution
- 3એક સ.આ. દોલકનો મહત્તમ વેગ અને મહત્તમ પ્રવેગ અનુક્રમે $\beta $ અને $\alpha $ છે, તો તેની આવૃત્તિ કેટલી હશે ?View Solution
- 4$10\, N$ ના બળ દ્વારા એક સ્પ્રિંગને $5\, cm$ જેટલી ખેંચવામાં આવે છે. જ્યારે $2\, kg$ નું દળ લટકાવવામાં આવે તો દોલનોનો આવર્તકાળ $.....\,s$ છે.View Solution
- 5$k$ બળ અચળાંક ધરાવતી સ્પ્રિંગના બે ટુકડા કરવામાં આવે છે,મોટા ટુકડાની લંબાઇ નાના ટુકડાની લંબાઇ કરતાં બમણી છે,તો મોટા ટુકડાનો બળ અચળાંક કેટલો થાય?View Solution
- 6સરળ આવર્તગતિ કરતાં પદાર્થView Solution
$(a)$ સ્થિતિઊર્જા હમેશા તેની ગતિઊર્જા જેટલી હોય.
$(b)$ ગમે તે સમય અંતરાલમાં સ્થિતિઊર્જા અને ગતિઊર્જાનું સરેરાશ મૂલ્ય સમાન થાય.
$(c)$ કોઈ પણ સમયે ગતિઊર્જા અને સ્થિતિઊર્જાનો સરવાળો અચળ હોય.
$(d)$ ગતિઊર્જાની એક આવર્તકાળપરની સરેરાશ સ્થિતિઊર્જાની એક આવર્તકાળપરની સરેરાશજેટલી હોય.
નીચે આપેલા વિકલ્પોમાંથી યોગ્ય વિકલ્પ પસંદ કરો
- 7એક લોલક ઘડિયાળ $40^o $ $C$ તાપમાને $12$ $s$ પ્રતિદિન ઘીમી પડે છે.તથા $20°$ $C$ તાપમાને $4$ $s$ પ્રતિદિન તેજ થાય છે.આ ઘડિયાળ સાચો સમય બતાવે તે તાપમાન તથા ઘડિયાળના લોલકની ધાતુનો રેખીય-પ્રસરણ ગુણાંક ($\alpha )$ ક્રમશ: છે.View Solution
- 8View Solutionસરળ આવર્તગતિમાં ગતિઊર્જા અને સ્થિતિઊર્જા કયાં સ્થાને સમાન થાય?
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે $m = 1.0\,kg$ નો પદાર્થ જમીન સાથે જડિત સ્પ્રિંગની ઉપર રહેલ પ્લેટફોર્મ પર મૂકવામાં આવે છે.સ્પ્રિંગ અને પ્લેટફોર્મનું દળ નહિવત છે. જો સ્પ્રિંગને થોડીક દબાવીને મુક્ત કરવામાં આવે તો તે સરળ આવર્ત ગતિ કરે છે. સ્પ્રિંગનો બળ અચળાંક $500\,N/m$ છે. આ ગતિ માટે કંપવિસ્તાર $A$ કેટલો હોવો જોઈએ કે જેથી $m$ દળ પ્લેટફોર્મથી છૂટો પડે?View Solution
($g = 10\,m/s^2$ અને ગતિ દરમિયાન સ્પ્રિંગ વિકૃત થતી નથી)
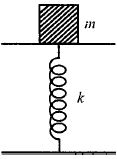
- 10આપેલ આકૃતિમાં, એક $M$ દળ જેનો એક છેડો દઢ આધાર સાથે જડિત કરેલ છે તેવી સમક્ષિતિજ સ્પ્રિંગ સાથે જોડેલ છે. સ્વિંગનો સ્પ્રિંગ અચળાંક $k$ છે. ઘર્ષણરહિત સપાટી પર દળ $T$ જેટલા આવર્તકાળ અને $A$ જેટલા કંપવિસ્તાર સાથે દોલન કરે છે. આકૃતિમાં દર્શાવ્યા અનુસાર, દળ જ્યારે સંતુલન સ્થિતિમાં હોય છે ત્યારે બીજા $m$ દળને ધીરેથી (સાવચેતીથી) તેના પર જોડવામાં આવે છે. દોલનનો નવો કંપવિસ્તાર ............ થશે.View Solution