किसी तार को खींचकर इसका व्यास आधा कर दिया जाता है। इसका नया प्रतिरोध का मान क्या होगा?
माना वास्तविक लम्बाई $=l_1$
वास्तविक व्यास $= d _1$
नयी लम्बाई $=l_2$
नया व्यास $= d _2$
खींचने के बाद तार का आयतन (या घनत्व) समान ही रहता है
अर्थात=
$A _1 l_1= A _2 l_2$
या $\frac{\pi d _1^2}{4} l_1=\frac{\pi d _2^2}{4} l_2$
या $l_2=\left(\frac{ d _1}{d_2}\right)^2 l_1$
$\because$ $d_2=\frac{1}{2} d_1$
$\because$ $\frac{d_1}{d_2}=\frac{2}{1}=2$
$l_2=(2)^2 l_1=4 l_1$
नयी लम्बाई $l_2=4 l_1$
हम जानते है $R =\rho \frac{l}{A}$
$\because$ $R _1=\frac{\rho \times 4 l_1}{\pi d _1^2}$
तथा $R _2=\frac{4 l_2 \rho}{\pi d _2^2}$
$\because$ $\frac{ R _2}{ R _1}=\frac{l_2 d_1^2}{l_1 d_1^2}$
$=\frac{4 l_1 d_1^2 \times 4}{l_1 \times d _1^2}=16$
नया प्रतिरोध $R_2=16 R_1$
अतः तार का नया प्रतिरोध प्रारम्भिक मान का 16 गुना हो जाएगा।
वास्तविक व्यास $= d _1$
नयी लम्बाई $=l_2$
नया व्यास $= d _2$
खींचने के बाद तार का आयतन (या घनत्व) समान ही रहता है
अर्थात=
$A _1 l_1= A _2 l_2$
या $\frac{\pi d _1^2}{4} l_1=\frac{\pi d _2^2}{4} l_2$
या $l_2=\left(\frac{ d _1}{d_2}\right)^2 l_1$
$\because$ $d_2=\frac{1}{2} d_1$
$\because$ $\frac{d_1}{d_2}=\frac{2}{1}=2$
$l_2=(2)^2 l_1=4 l_1$
नयी लम्बाई $l_2=4 l_1$
हम जानते है $R =\rho \frac{l}{A}$
$\because$ $R _1=\frac{\rho \times 4 l_1}{\pi d _1^2}$
तथा $R _2=\frac{4 l_2 \rho}{\pi d _2^2}$
$\because$ $\frac{ R _2}{ R _1}=\frac{l_2 d_1^2}{l_1 d_1^2}$
$=\frac{4 l_1 d_1^2 \times 4}{l_1 \times d _1^2}=16$
नया प्रतिरोध $R_2=16 R_1$
अतः तार का नया प्रतिरोध प्रारम्भिक मान का 16 गुना हो जाएगा।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionधातु इलेक्ट्रॉनों के अपवाह वेग का मान अति लघु क्यों होता है?
- 2View Solutionचित्र में दर्शाये गये जालक के बिन्दु a व b के मध्य तुल्य प्रतिरोध का मान ज्ञात कीजिए।
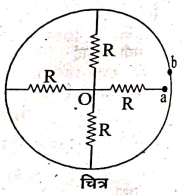
- 3View Solutionचित्र में असमान काट क्षेत्रफल का एक धारावाही चालक दर्शाया गया है। किन बिन्दुओं पर मान अंधिकतम होगा। (अ) धारा का (ब) धारा घनत्व का तथा (स) अपवहन वेग का।

- 4View Solutionअपवहन वेग को समझाइए। विद्युत धारा तथा अपवहन वेग मे सम्बन्ध स्थापित कीजिए। परिपथ चित्र बनाकर परिपथ में प्रवाहित इलेक्ट्रॉन की दिषा दर्षाइए।
- 5View Solutionकिरखोफ का संधि नियम लिखिए।
दिए गये चित्र में धारा I का मान लिखिए-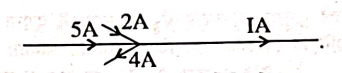
- 6एक इलेक्ट्रॉन वृत्ताकार कक्षा में $6 \times 10^{15}$ बार प्रति सेकण्ड घूमता है। लूप में धारा का मान ज्ञात कीजिए।View Solution
- 7View Solutionअपवहन वेग को समझाइए। विद्युत धारा तथा अपवहन वेग मे सम्बन्ध स्थापित कीजिए। परिपथ चित्र बनाकर परिपथ में प्रवाहित इलेक्ट्रॉन की दिषा दर्षाइए।
- 80.24 मीटर लम्ब चालक के सिरों के बीच 6 वोल्ट का विमवान्तर लगाया गया है। इलेक्ट्रॉनों का अनुगमन (अपवाह) वेग ज्ञात कीजिए। इलेन्ट्रॉन की गतिशीलता $5.6 \times 10^{-6}$ मीटर $^2$ वोल्ट ${ }^{-1}$ सेकण्ड $^{-1}$ है।View Solution
- 9एक 15$\Omega$ के मोटे तार को खींचकर इसकी लम्बाई को तीन गुना कर दिया जाता है। यह मानते हुए कि खींचने पर इसका घनत्य अपरिवर्तित रहता है। नए तार के प्रतिरोध की गणना कीजिए।View Solution
- 10एक तार की अनुप्रस्थ काट का क्षेत्रफल $1.0 \times 10^{-7}$ मीटर $^2$ तथा तार में मुक्त इलेक्ट्रॉनों की संख्या $2 \times 10^{28}$ प्रति मीटर ${ }^3$ है। तार मे $3.2$ एंपायर की धारा प्रवाहित हो रही है। ज्ञात कीजिये $(i) $तार मे धारा धनत्व$, (ii)$ मुक्त एलेक्ट्रोनों का अपवहन वेग।View Solution
