$\ln k =10-\frac{69( KJ )}{ RT } \cdots \cdots( i )$
$k=A e^{-E_{a} / R T}$
$\ln k=\ln A-\frac{E_{a}}{R T} \cdots \cdots(i i)$
Comparison of equation $(i)$ and $(ii)$
$E_{a}$ is $69$
The rate constants in Arrhenius equation at two different
temperatures are expressed as stated below
$\ln k_{1}=\ln A-\frac{E_{ a }}{ RT _{1}}$
$\ln k_{2}=\ln A-\frac{E_{ a }}{ RT _{2}}$
Therefore, the Arrhenius equation for two different temperatures is expressed as shown below.
$\ln k_{2}-\ln k_{1}=\left(\ln A-\frac{E_{ a }}{ RT _{2}}\right)-\left(\ln A-\frac{E_{ a }}{ RT _{1}}\right)$
This equation is simplified as shown below.
$\ln \frac{k_{2}}{k_{1}}=\frac{E_{2}}{ R }\left(\frac{1}{ T _{1}}-\frac{1}{ T _{2}}\right)$
$\ln \frac{k_{2}}{k_{1}}=\frac{E_{ a }}{ R }\left(\frac{ T _{2}- T _{1}}{ T _{1} T _{2}}\right)$ or $\log \frac{k_{2}}{k_{1}}=\frac{E_{ a }}{2.303 R }\left(\frac{ T _{2}- T _{1}}{ T _{1} T _{2}}\right)$
Substitute the values in the above equation as follows.
$\log \frac{2 k_{1}}{k_{1}}=\frac{69}{2.303 \times 8.314}\left(\frac{ T _{2}-300}{300 T _{2}}\right)$
$\log 2=\frac{69 \times 10^{3}}{2.303 \times 8.314}\left(\frac{ T _{2}-300}{300 T _{2}}\right)$
$T _{2}=307.7 \,K$
Download our appand get started for free
Similar Questions
- 1કાલ્પનિક પ્રક્રિયા $A_2 + B_2 \rightarrow2AB$ નીચે મુજબ ક્રિયાવિધી દર્શાવે છે. તો બધી જ પ્રક્રિયાનો ક્રમ .... થાય.View Solution
$A_2 $ $\rightleftharpoons$ $ A + A$ ....... (ઝડપી) ;
$A + B_2\rightarrow AB + B$ ..... (ધીમી) ;
$ A + B \rightarrow AB$ ...... (ઝડપી)
- 2$Kt = lnC_0 - lnC_t$ સમીકરણમાં $ t$ અને $lnC_t$ વચ્ચેનો વક્ર ..... માં હોય.View Solution
- 3ઉષ્માક્ષેપક પ્રક્રિયા $A \rightarrow B$ માટે $A$ ની સક્રીયકરણ ઊર્જા $17\, kJ$ પ્રતિ મોલ છે. પ્રક્રિયાની ઉષ્મા $40 \,kJ$ છે. તો પ્રતિવર્તીં પ્રક્રિયા $B \rightarrow A$ માટેની સક્રીયકરણ ઊર્જા ગણો.View Solution
- 4View Solutionનીચેનામાંથી ક્યુ વિધાન ખોટુ છે ?
- 5પ્રક્રિયાનો વેગ અચળાંક $(k)$ જુદા-જુદા તાપમાન $(T)$ પર માપવામાં આવે છે અને આપેલ આકૃતિમાં માહિતી આલેખ દ્વારા આપવામાં આવેલ છે.પ્રક્રિયાની સક્રિયકરણ ઊર્જા $kJ\, mol ^{-1}$માં થશે?View Solution
($R$ એ વાયુ અચળાંક છે)
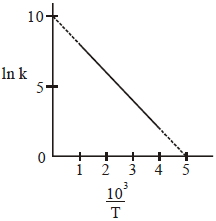
- 6ક્ષય અચળાંક $2.25\times 10^{-4 }$ વર્ષ$^{-1}$ ધરાવતા $_{6}^{14}C$ નો અર્ધઆયુષ્ય સમય .......... વર્ષ હશે.View Solution
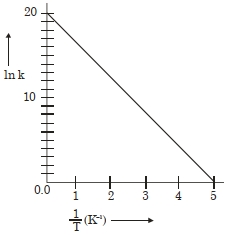
- 7એક પ્રક્રિયા માટે, $\ln K$ વિરુદ્ધ $\frac{1}{ T }$ નો આલેખ નીચે આપેલો છે. પ્રક્રિયાની સક્રિયકરણ ઊર્જા $......cal$ $mol ^{-1}$ (નજીકના પૂર્ણાંક)View Solution
(આપેલું છે: $R =2\,cal\,K ^{-1}\,mol ^{-1}$ )
- 8પાણી પર થતી પ્રક્રિયા માટે, પ્રક્રિયાનો ક્રમ કયો છેView Solution
${{H}_{2}}+C{{l}_{2}}\xrightarrow{\text{Sunlight}}2HCl$
- 9View Solutionનીચેનામાંથી ક્યુ વિધાન સાચું છે ?
- 10$373\,K$ એ વાયુમય પ્રક્રિયા $A \rightarrow 2B + C$ પ્રથમ ક્રમની પ્રક્રિયા મળે છે. શુદ્ધ $A$ નું શરૂઆત કરતાં તે $10$ મિનિટ પછી પ્રણાલીનું કુલ દબાણ $176\,mm $ મક્યુરી અને લાંબા સમય પછી જ્યારે તે $270\,mm$ થાય છે તો ઉપરની માહિતી પરથી $(1)\,A$ નું પ્રારંભિક દબાણ $(2)\,A $ નું $10 $ મિનિટ પછીનું દબાણ $(3)$ દર અચળાંકની ગણતરી ... ....View Solution
