ધારો કે $A$ નું પ્રારંંભિક દબાણ $= A = P\,mm.$
$A $ નું દબાણ $t$ સમય પછી ઘટે છે. $t = P\,mm.$
$A \rightarrow 2B + C$ કુલ દબાણ
પ્રારંભિક દબાણ $P_0$ $0$ $0$ $P_0 $
$t $ સમય પછીનું દબાણ $P_0 - x$ $2x$ $x$ $P_0 + 2x$
અંંતિમ દબાણ $0$ $2P_0$ $P_0$ $3P_0$
$(1)$ અંતિમ દબાણ $= 270\,mm $ (આપેલ)
$3P_0 = 270 $ અથવા $ P_0 = 90\,mm$
$(2)$ $10$ મિનિટ પછી $A$ નું દબાણ $=$ $176 \,mm$ (આપેલ)
$P_0 + 2x = 176$ અથવા $90 + 2x = 176.$
અથવા $x = 43\,mm$
$10$ મિનિટ પછી $A$ નું દબાણ $= P_0 - x = 90 - 43 = 47\,mm$
$(3)\,\,a\,\,\alpha \,\,{P_0}$
$\therefore $ $k=\frac{2.303}{t}\log \frac{a}{a-x}$ $=\frac{2.303}{t}\log \frac{{{P}_{0}}}{{{P}_{0}}-x}$
અથવા
$=\,\frac{2.303}{10}\log \frac{90}{90-43}$
$=\frac{2.303}{10}\log \frac{90}{47}$
$=6.496\times {{10}^{-2}}\,{{\min }^{-1}}$
Download our appand get started for free
Similar Questions
- 1કાર્બનિક ક્લોરાઇડનું જળવિભાજન વધુ પ્રમાણમાં પાણીની હાજરીમાં નીચે પ્રમાણે કરવામાં આવે છે. $R - Cl + H_2O \rightarrow R - OH + HCl $ તો નીચેના પૈકી કયો વિકલ્પ સાચો છે ?View Solution
- 2પ્રથમ ક્રમની પ્રક્રિયા માટે, ધન ઢાળ મેળવવા માટે કયા ઢાળ ની જરૂર છે( જ્યાં $[A]$ એ પ્રકીયક ની સાંદ્રતા $A$)View Solution
- 3View Solutionનીચેના માંથી કઇ પ્રક્રિયામાં દબાણના ફેરફારથી પ્રક્રિયા-વેગમાં ફેરફાર થશે નહિ ?
- 4પ્રક્રિયા${H_{2\left( g \right)}} + {I_{2\left( g \right)}} \to 2H{I_{\left( g \right)}}$ માટેની શક્ય ક્રિયાવિધિ નીચે મુજબ છે.View Solution
${I_2}\,\underset{{{K_{ - 1}}}}{\overset{{{K_1}}}{\longleftrightarrow}}\,2I\,$ (fast step)
$2I + {H_2}\xrightarrow{{{K_2}}}2HI$ (slow step)
તો પ્રક્રિયાનો વેગનિયમ જણાવો.
- 5પ્રથમ ક્રમની પ્રક્રિયા માટે અર્ધઆયુષ્ય સમય $6$ મિનિટ છે. તો પ્રક્રિયાનો દર અચળાંક શોધો.View Solution
- 6View Solutionઓરડાના તાપમાને હાઇડ્રોજન અને ઓક્સિજનનુ મિશ્રણ ખૂબ સ્થાયી છે. પરંતુ સ્પાર્ક કરવાથી તરત જ વિસ્ફોટ થાય છે. કારણ કે .........
- 7એક પ્રથમક્રમ પ્રક્રિયા $A \rightarrow$ નીપજો માટે, $A$ની પ્રારંભિક સાંદ્રતા $0.1\,M$ છે, જે $5$ મિનિટો પછી $0.001 \,M$ થાય છે. પ્રક્રિયા માટે વેગ અચળાંક $min ^{-1}$માં શોધો.View Solution
- 8જો તાપમાન $20\,^oC$ થી વધી $35\,^oC$ થતા પ્રક્રિયાનો વેગ બે ગણો થતો હોય તો પ્રક્રિયાની સક્રિયકરણ ઊર્જા ........... $kJ \,mol^{-1}$ થશે.View Solution
$(R = 8.314\, J \,mol^{-1}\, K^{-1})$
- 9નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.View Solution
$\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$
પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.
સ્ટેપ Rate constant $\left(\sec ^{-1}\right)$
Activation energy
$\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$
$1$ ${k}_1$ $300$ $2$ ${k}_2$ $200$ $3$ ${k}_3$ $\mathrm{Ea}_3$ ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).
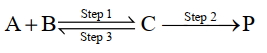
- 10નીચેની પ્રક્રિયા માટે: $NO_2(g) + CO(g) \to NO(g) + CO_2(g)$, દર નિયમ : દર $= k \,[NO_2]^2$ છે. જો વાયુયુક્ત કાર્બન મોનોક્સાઇડનો $0.1$ મોલ પ્રક્રિયા મિશ્રણમાં અચળ તાપમાને ઉમેરવામાં આવે તો નીચેનામાંથી કયું વિધાન સાચું છે?View Solution
