$l$ લંબાઈના એક હલકા સળિયાનાં બંને છેડે $m_1 $ અને $m_2$ દ્રવ્યમાનના પદાર્થો લગાડેલાં છે. આ સળિયાને લંબ તથા તેના દ્રવ્યમાનકેન્દ્રની અક્ષમાંથી પસાર થતી અક્ષને અનુલક્ષીને તંત્રની જડત્વની ચાકમાત્રા કેટલી થાય?
NEET 2016, Medium
c
Here,\({l_1} + {l_2} = l\)
Here,\({l_1} + {l_2} = l\)
Center of mass of the system,
\({l_1} = \frac{{{m_1} \times 0 + {m_2} \times l}}{{{m_1} + {m_2}}} = \frac{{{m_2}l}}{{{m_1} + {m_2}}}\)
\({l_2} = l - {l_1} = \frac{{{m_1}l}}{{{m_1} + {m_2}}}\)
Required moment of inertia of the system,
\(I = {m_1}l_1^2 + {m_2}l_2^2\)
\(= \left( {{m_1}m_2^2 + {m_2}m_1^2} \right)\frac{{{l^2}}}{{{{\left( {{m_1} + {m_2}} \right)}^2}}}\)
\(= \frac{{{m_1} + {m_2}\left( {{m_1} + {m_2}} \right){l^2}}}{{{{\left( {{m_1} + {m_2}} \right)}^2}}} = \frac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}{l^2}\)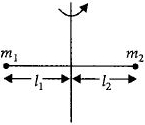
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
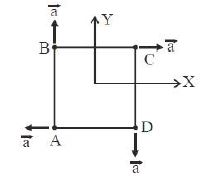
- 1ચોરસના ચાર બિંદુ પર ચાર કણ $A, B, C$ અને $D$ જેના દળ $m_A=m, m_B=2m, m_C=3m$ અને $m_D=4m$ મૂકેલા છે.આકૃતિમાં દર્શાવ્યા પ્રમાણેની સમાન મૂલ્યના પ્રવેગથી ગતિ કરે તો તેના દ્રવ્યમાન કેન્દ્રનો પ્રવેગ કેટલો થાય?View Solution
- 2એક કણ $a$ ત્રિજયાના વર્તુળ પર અચળ ઝડપથી ગતિ કરે છે.$AB$ વ્યાસ અને $C$ કેન્દ્ર છે.તો કણ $B$ પર હોય,ત્યારે $A$ અને $C$ ને અનુલક્ષીને કોણીય ઝડપનો ગુણોત્તર કેટલો થાય?View Solution
- 3View Solutionએક નક્કર ગોળો અવકાશમાં ચાકગતિ કરી રહ્યો છે, જો ગોળાનું દળ અચળ રાખીને તેની ત્રિજ્યા વધારવામાં આવે, તો નીચેનામાંથી કઈ ભૌતિક રાશિ બદલાશે નહિ ?
- 4$2\ kg $ દળ ધરાવતો પદાર્થ એ $2\ m$ ત્રિજ્યા ધરાવતા વર્તૂળમાર્ગ પર નિયમિત ગતિ કરે છે. જો તેના પર લાગતું કેન્દ્રગામી બળ $100\ N$ હોય, તો તેનું કોણીય વેગમાન ....... $J s $ થાય.View Solution
- 5$200 g$ અને $500 g$ દળવાળા કણો $10\,\hat i\,\,m/s\,$ અને $3\,\hat i + 5\,\hat j\,\,m/s $ અનુક્રમે ના વેગથી ગતિ કરે છે, તો કણોથી બનતા તંત્રના દ્રવ્યમાન કેન્દ્ર નો વેગ .................. થાય.View Solution
- 6$R$ ત્રિજયા અને $M$ દળ ધરાવતી એક નિયમિત વર્તુળાકાર તકતીને લંબ એવી રીતે તેની ધારમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 7$M$ દ્રવ્યમાન તથા $R$ ત્રિજયાની એક તકતી પર $R$ વ્યાસનો વર્તુળાકાર ભાગ એવી રીતે કાપવામાં આવે છે, કે જેથી તેનો પરિઘ તકતીના કેન્દ્રમાંથી પસાર થાય. તકતીના બાકીના ભાગનો, તકતીના કેન્દ્રમાંથી પસાર થતી અને તેને લંબ એવી અક્ષને અનુલક્ષીને તેની જડત્વની ચાકમાત્રા શું થશે?View Solution
- 8દળમાં ફેરફાર વગર જો પૃથ્વીની ત્રિજ્યા તેના વર્તમાન મૂલ્ય કરતાં $n$ ગણી થઈ જાય તો દિવસનો સમયગાળો કેટલો છે ?View Solution
- 9એક $100\, m$ ઊંચા મકાનની ટોચ પર થી $0.03\, kg$ દળ ધરાવતા એક લાકડાના ટુકડાને મુક્ત કરવામાં આવે છે. આ જ સમયે, $0.02\, kg$ દળ ધરાવતી ગોળી (કારતુસ ) ને જમીન પરથી ઊર્ધ્વદિશામાં ઊપર તરફ $100 \,ms^{-1}$ ના વેગ થી છોડવામાં આવે છે. ગોળી લાકડામાં જોડાઈ જાય છે, તો આ સંયુક્ત તંત્રે પાછું પડવાનું ચાલુ કરે તે પહેલા મકાનની ટોચથી ઊપર પહોંચેલ મહત્તમ ઊંચાઈ ........ $m$ થશે. $(g=10 \,m/s^2)$View Solution
- 10$m = 2$ દળ ધરાવતો કણ સમયની સાપેક્ષે $\vec r\,(t)\, = \,2t\,\hat i\, - 3{t^2}\hat j$ મુજબ ગતિ કરે છે.$t = 2$ સમયે ઉગમબિંદુની સાપેક્ષે કોણીય વેગમાન કેટલુ થાય?View Solution
