Just before collision speed of \(m\)
\(v = \sqrt {2gL\left( {1 - \cos {\theta _ \circ }} \right)} \)
Just after collision speed os \( M \)
\({v_1} = \sqrt {2gL\left( {1 - \cos {\theta _1}} \right)} \)
\(\begin{array}{l}
And\,{v_1} = \left( {\frac{{M - m}}{{M + m}}} \right)v\,\,;\,\,\frac{{{v_1}}}{v} = \frac{{M - m}}{{M + m}}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\sqrt {\frac{{1 - \cos {\theta _1}}}{{1 - \cos {\theta _0}}}} = \frac{{M - m}}{{M + m}}\\
\frac{{\sin \left( {{\theta _1}/2} \right)}}{{\sin \left( {{\theta _0}/2} \right)}} = \frac{{M - m}}{{M + m}}\,\,\,\,\,\left[ {1 - \cos 2\theta = 2{{\sin }^2}\theta } \right]\\
\frac{{{\theta _1}}}{{{\theta _0}}} = \frac{{M - m}}{{M + m}}
\end{array}\)
\(\begin{array}{l}
M{\theta _1} + m{\theta _1} = M{\theta _0} - m{\theta _0}\\
M = m\left[ {\frac{{{\theta _1} + {\theta _0}}}{{{\theta _0} - {\theta _1}}}} \right]
\end{array}\)
Download our appand get started for free
Similar Questions
- 1$m$ દળનો ગોળો $u$ વેગથી $m $ દળના સ્થિર ગોળાને અથડાય છે,જો રેસ્ટીંટયુશન ગુણાંક $e$ હોય,તો સંધાત પછી બંને ગોળાના વેગનો ગુણોત્તર કેટલો થાય?View Solution
- 2એક ગાડીને $10 m/s$ થી $20 m/s $ સુધી પ્રવેગી કરવા માટે જરૂરી ઊર્જાએ સ્થિર સ્થિતિએ રહેલી ગાડીને $10 m/s$ જેટલી પ્રવેગીત કરવા માટે જરૂરી ઊર્જા કેટલા ગણી છે?View Solution
- 3એક કણ $4\,\hat i\,\, + \,\,\hat j\,\, + \,\,3\hat k$ બળની અસર હેઠળ $\mathop {{r_1}}\limits^ \to \,\, = \,\,3\,\hat i\,\, + \,\,2\,\hat j\,\, - \,\,6\hat k$ સ્થાનથી $\mathop {{r_2}}\limits^ \to \, = \,\,14\,\hat i\,\, + \,\,13\,\hat j\,\, + \,\,9\hat k$ સ્થાન સુધી ગતિ કરે છે. તો થતું કાર્ય.....$J$ માં શોધો.View Solution
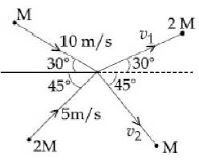
- 4$M$ અને $2M$ દળ અને $10\, m/s$ અને $5\, m/s$ વેગ ધરાવતા બે કણ ઉગમબિંદુ પાસે સ્થિતિસ્થાપક અથડામણ અનુભવે છે.અથડામણ પછી બંને આકૃતિમાં દર્શાવ્યા મુજબ $v_1$ અને $v_2$ વેગથી ગતિ કરે તો $v_1$ અને $v_2$ અનુક્રમે કેટલા મળે?View Solution
- 5$M = 5 kg$ દળનો બ્લોક સ્પ્રિંગના એક છેડે લટકાવેલો છે. આ સ્પ્રિંગ શિરોલંબ દિશામાં $l = 0.1 m$ જેટલું બ્લોકના દળના કારણે વિસ્તરણ પામે છે. બ્લોકને $v = 2 m/sec$ ની ઝડપ ઊર્ધ્વ દિશામાં આપવામાં આવે છે. બ્લોક કેટલા ............. $\mathrm{m}$ ઉંચાઈએ પહોંચશે ? ($g = 10 m/s^2$)View Solution
- 6એક બોલ સ્થિર સ્થિતિએ રહેલા તેના કરતા બમણું દળ ધરાવતા બોલ સાથે $1.5 m/s $ ના વેગથી હેેડઓન સંઘાત કરે છે. જો રેસ્ટીટ્યૂશન ગુણાંક $0.6$ હોય તો અથડામણ પછી તેઓનો વેગ કેટલો હશે ?View Solution
- 7સ્થિર સ્થિતિમાં રહેલો એક કણ એ $x$ અને $y$ દળનાં બે કણોમાં વિસ્ફોટ પામે છે. જેઓ એકબીજાથી વિરુદ્ધ દિશામાં $v_1$ અને $v_2$ વેગ સાથે ગતિ કરે છે. તેમની ગતિઉર્જાઓ $\left(E_1: E_2\right)$ નો ગુણોત્તર છેView Solution
- 8View Solutionબ્લોકને અચળ પાવરથી ખસેડતા તેને કાપેલ અંતર સમયનાં પર કઈ રીતે આધાર રાખે?
- 9$L = \frac{{10}}{3}\,m$ લંબાઇની દોરી સાથે $1\,kg$ નો પદાર્થ બાંધીને શિરોલંબ વર્તુળાકાર પથ પર ભ્રમણ કરવવામાં આવે છે.દોરીમાં મહત્તમ અને ન્યુનતમ તણાવનો ગુણોત્તર $4$ છે,તો પદાર્થની મહત્તમ ઊંચાઇના બિંદુએ ઝડપ ...... $m/\sec$ હશે.View Solution
- 10$100 m $ લંબાઇ અને $1 m$ ઉંચાઇ ધરાવતા ઢાળ પર $30,000 kg$ નો ટ્રક $30 km/hr$ ની ઝડપથી ગતિ કરે,તો ટ્રકનો પાવર કેટલા .......... $kW$ થશે? $( g = 10m{s^{ - 1}}) $View Solution
