$L = \frac{{10}}{3}\,m$ લંબાઇની દોરી સાથે $1\,kg$ નો પદાર્થ બાંધીને શિરોલંબ વર્તુળાકાર પથ પર ભ્રમણ કરવવામાં આવે છે.દોરીમાં મહત્તમ અને ન્યુનતમ તણાવનો ગુણોત્તર $4$ છે,તો પદાર્થની મહત્તમ ઊંચાઇના બિંદુએ ઝડપ ...... $m/\sec$ હશે.
Diffcult
d
(d) Since the maximum tension \({T_B}\) in the string moving in the vertical circle is at the bottom and minimum tension \({T_T}\) is at the top.
(d) Since the maximum tension \({T_B}\) in the string moving in the vertical circle is at the bottom and minimum tension \({T_T}\) is at the top.
\({T_B} = \frac{{mv_B^2}}{L} + mg\) and \({T_T} = \frac{{mv_T^2}}{L} - mg\)
\(\frac{{{T_B}}}{{{T_T}}} = \frac{{\frac{{mv_B^2}}{L} + mg}}{{\frac{{mv_T^2}}{L} - mg}} = \frac{4}{1}\) or \(\frac{{v_B^2 + gL}}{{v_T^2 - gL}} = \frac{4}{1}\)
or \(v_B^2 + gL = 4v_T^2 - 4gL\) but \(v_B^2 = v_T^2 + 4gL\)
\(v_T^2 + 4gL + gL = 4v_T^2 - 4gL\)==> \(3v_T^2 = 9gL\)
\(v_T^2 = 3 \times g \times L = 3 \times 10 \times \frac{{10}}{3}\) or \({v_T} = 10\,m/\sec \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $2 \,kg$ દળનાં કણની સ્થિતિ ઊર્જા $(PE)$ એ વાળા $x$-અક્ષ $U(X)=\left(\frac{x^3}{3}-\frac{x^2}{2}\right)\, J$ વડે આપેલ છે. કણની કુલ યાત્રિક ઊર્જા $4 \,J$ છે. તો મહતમ ઝડપ $\left( ms ^{-1}\right.$ માં) કેટલી હશે?View Solution
- 2$4m$ દ્રવ્યમાનના અને $u$ ઝડપતી ગતિ કરતો એક પદાર્થ $A$ એ $2m$ દ્રવ્યમાનના અને સ્થિર એવા એક પદાર્થ $B$ સાથે અથડાય છે. આ અથડામણ હેડ ઓન અને સ્થિતિસ્થાપક પ્રકૃતિની છે. અથડામણ પછી પદાર્થ $A$ વડે ગુમાવાતી ઊર્જાનો જથ્થો કેટલો હશે?View Solution
- 3એક કણ સમતલમાં $\overrightarrow{ F }=\left(4 x \hat{i}+3 y^{2} \hat{j}\right)$ જેટલું ચલ બળ અનુભવે છે. અંતર મીટરમાં અને બળ ન્યૂટનમાં છે તેમ ધારો. જો કણ $x-y$ સમતલમાં બિંદૂ $(1,2)$ થી $(2,3)$ આગળ ખસે તો ગતિઉર્જા...........$J$ જેટલી બદલાશે.View Solution
- 4View Solutionજો એક પદાર્થ સ્થિર સ્થિતિએ રહેલા તેટલાજ દળના પદાર્થ સાથે અસ્થિતિ સ્થાપક રીતે અથડાય છે સંઘાત પછી તેઓની ઝડપનો ગુણોત્તર શું હશે ?
- 5$1\, m$ ઊંચાઈ ધરાવતા ટેબલ પર એક $1.9\, kg$ દળનો બ્લોક પડેલો છે. $0.1\, kg$ ધરાવતી ગોળી આ બ્લોક સાથે અથડાય અને તેની સાથે જોડાઈ જાય છે. જો અથડાતાં પહેલા આ ગોળીનો સમક્ષિતિજ દિશામાં વેગ $20\, m / s$ હોય તો પછી બ્લોક જ્યારે જમીન સાથે અથડાય તેની પહેલા આ જોડાયેલા તંત્રની ગતિઉર્જા કેટલા $J$ હશે?View Solution
$[g =10\, m / s ^{2}$. ધારો કે તેમાં કોઈ ચાક ગતિ નથી અને અથડામણ પછી ઉર્જાનો વ્યય નહિવત છે.$]$
- 6એક અચળ $F$ ની અસર હેઠળ સ્થિર અવસ્થાથી શરૂ કરી $m$ દળે એક નિયત અંતર $d$ કાપવા દરમિયાન શરૂ થઈને $l$ જેટલું નિશ્ચિત અંતર કાપવા દરમિયાન $m$ દળે મેળવેલી ગતિ ઉર્જાView Solution
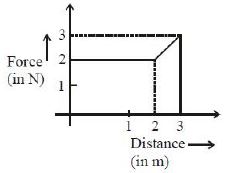
- 7ગ્રાફમાં દર્શાવ્યા પ્રમાણે એક કણ આપેલ સ્થાન સાથે બદલાતા બળના કારણે એક પારિમાણિક ગતિ કરે છે. $3\, m$ ગતિ કર્યા પછી કણની ગતિઉર્જા કેટલા .............. $\mathrm{J}$ થશે?View Solution
- 8જેનો રેસ્ટીટ્યૂશન ગુણાંક $0. 5 $ હોય તેવા એક બોલને અમુક ઉંચાઈએ છોડતા તેના દરેક ઉછળાટનો પ્રતિશત ઊર્જા ક્ષય કેટલા........$\%$ હશે?View Solution
- 9View Solutionજ્યારે બે કણો અથડાય છે ત્યારે સામાન્ય રીતે શું સાચું હશે?
- 10$x$ અક્ષની દિશામાં મુક્ત રીતે ગતિ કરતા $1 kg $ દળના કણની સ્થિતિ ઊર્જા $V(x)\,\, = \,\,\left( {\frac{{{x^4}}}{4}\, - \,\,\frac{{{x^2}}}{2}} \right)\,J$સૂત્રથી આપી શકાય કણની કુલ યાંત્રિક ઊર્જા $2 J $ છે. તો કણની મહત્તમ ઝડપથી $ (m/s)$ માં કેટલી હશે ?View Solution
