લંબાઈ $L$ ની એક પાતળી પટ્ટી માટે એકમ લંબાઈ દીઠ દળ $\lambda $ માં એક છેડા તરફથી અંતર વધતાં રેખીય વધારો થાય છે. જો તેનું કુલ દળ $M$ અને હળવા છેડે એકમ લંબાઈ દીઠ દળ $\lambda_0$ હોય તો હળવા છેડે થી દ્રવ્યમાન કેન્દ્રનું અંતર કેટલું હશે?
JEE MAIN 2014, Diffcult
c
Mass per unit lengh \(=\lambda_{0}+\mathrm{kx}\)
Mass per unit lengh \(=\lambda_{0}+\mathrm{kx}\)
\(\mathrm{M}=\int_{0}^{\mathrm{L}}\left(\lambda_{0}+\mathrm{kx}\right) \mathrm{dx}\)
\(M=\lambda_{0} L+\frac{K \times L^{2}}{2}\)
\(\frac{2 \mathrm{M}-\lambda_{0} \mathrm{L}}{\mathrm{L}^{2}}=\mathrm{K}\)
\(\frac{2 \mathrm{M}}{\mathrm{L}^{2}}-\frac{\lambda_{0}}{\mathrm{L}}=\mathrm{K}\)
\(\frac{\int \mathrm{d} \mathrm{m}(\mathrm{r})}{\int \mathrm{d} \mathrm{m}}=\frac{\int(\lambda \mathrm{d} n) \mathrm{x}}{\mathrm{M}}=\frac{\int_{0}^{\mathrm{L}}\left(\lambda_{0} \mathrm{x}+\mathrm{k} \mathrm{x}^{2}\right) \mathrm{d} \mathrm{x}}{\mathrm{M}}\)
\(r_{c m}=\frac{\lambda_{0} L+\frac{k L^{2}}{2}}{M}\)
substitute \('k"\)
\(r_{c m}=\frac{2 L}{3}-\frac{\lambda_{0} \ell^{2}}{6 M}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2\,kg$ દ્રવ્યમાન ધરાવતો ધનગોળો સમક્ષિતિજ પૃષ્ઠ પર $2240\,J$ ગતિઉર્જા સાથે શુદ્ધ લોટણ ગતિ કરે છે. તો ગોળાના કેન્દ્રનો વેગ $............ms ^{-1}$ હશે.View Solution
- 2$50\ cm$ લંબાઇના એક સળીયાને એક છેડાથી જડેલ છે. આ સળીયાને સમક્ષિતિજ સાથે $30^o$ ના ખૂણે આકૃતિમાં બતાવ્યા પ્રમાણે ઊંચકીને સ્થિર અવસ્થામાંથી મુક્ત કરવામાં આવે છે. આ સળીયો જ્યારે સમક્ષિતિજને પસાર કરશે ત્યારે તેની કોણીય ઝડપ ($rad\, s^{-1}$ માં) થશેView Solution
- 3View Solutionફલાય વ્હીલ તેની અક્ષ પર અચળ કોણીય વેગથી ચાકગતિ કરે છે. જો અચાનક કોઈ પદાર્થ તેની રીંગ પર ચોટી જાય ત્યારે જડત્વની ચાકમાત્ર શું થશે ?
- 4બે વર્તૂળાકાર રિંગના દળોનો ગુણોત્તર $1 : 2$ અને વ્યાસોનો ગુણોત્તર $ 2 : 1$ છે. તો તેમની જડત્વની ચાકમાત્રાનો ગુણોત્તર શું હોય?View Solution
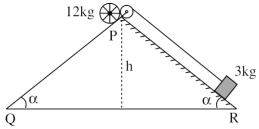
- 5$12 \,kg$ નું એક ગગડતું પૈડું ઢળતા સમતલ (ઢોળાવ) પર $P$ સ્થાને છે અને દોરી અને પુલી વડે $3 \,kg$ ના દળ સાથે આકૃતિમાં દર્શાવ્યા અનુસાર જોડેલ છે. ધારો કે $PR$ એ ધર્ષણરહિત સપાટી છે. જ્યારે વ્હીલ ઢોળાવમાં $PQ$ ના તળિયે $Q$ આગળ પહોંચે છે ત્યારે તેના ટ્રવ્યમાન કેન્દ્રની વેગ $\frac{1}{2} \sqrt{x g h} \,m / s$ છે. $x$ નું મૂલ્ય ..............View Solution
- 6એક કણનો સ્થાનસદિશ $\mathop r\limits^ \to = (\hat i + 2\hat j - \hat k)$ અને વેગમાન $\mathop P\limits^ \to = (3\hat i + 4\hat j - 2\hat k)$ છે. આ કણનો કોણીય વેગમાન ..... ને લંબ થાય.View Solution
- 7View Solutionકોઈ પદાર્થના જડત્વની ચાકમાત્રા શેના ઉપર આધાર રાખે છે?
- 8જો એક તકતીની તેની અક્ષ ને આધારે જડત્વની ચાકમાત્રા $I$ હોય તો તેના તેજ સમતલમાં રહેલા સ્પર્શક ના આધારે તેની જડત્વની ચાકમાત્રા કેટલી થાય $?$View Solution
- 9View Solutionકોઈ બાહ્ય ટોર્ક ની ગેરહાજરી માં જ્યારે એક પદ્રાર્થ તેની અક્ષ ઉપર ભ્રમણ કરી રહ્યો હોય તો નીચેના માંથી ખોટું નિવેદન પસંદ કરો.
- 10$100\,kg$ દળનો માણસ એ $200\,kg$ ના પ્લેટફોર્મ પર ઉભો છે. જે સૂવાળી બરફની સપાટી પર છે. જો માણસ પ્લેટફોર્મ પર $30\,m / s$ ના વેગથી ગતિ કરે છે, તો $..........m/s$ વેગથી પ્લેટફોર્મ એ બરફની સાપેક્ષમાં પાછુ ખસશે.View Solution
