$2\,kg$ દ્રવ્યમાન ધરાવતો ધનગોળો સમક્ષિતિજ પૃષ્ઠ પર $2240\,J$ ગતિઉર્જા સાથે શુદ્ધ લોટણ ગતિ કરે છે. તો ગોળાના કેન્દ્રનો વેગ $............ms ^{-1}$ હશે.
JEE MAIN 2023, Medium
Download our app for free and get started
a
\(KE =\frac{1}{2} mv ^2+\frac{1}{2} I \omega^2\)
\(KE =\frac{1}{2} mv ^2+\frac{1}{2} I \omega^2\)
\(2240=\frac{1}{2} 2( v )^2+\frac{1}{2} \frac{2}{5}(2) R ^2 \cdot\left(\frac{ v }{ R }\right)^2\)
\(2240= v ^2+\frac{2}{5} v ^2\)
\(\Rightarrow v =40\,m / s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1દોરી ધરાવતી એક ગરગડીને છત પર નીપત કરેલી છે તેના બંને છેડા આગળ $m $ અને $3m$ દળના પદાર્થ જોડેલો છે. જો ગરગડી અને દોરીનું વજન અવગણ્ય છે અને તે ઘર્ષણ રહીત છે તંત્રનું દ્રવ્યમાન કેન્દ્રનો પ્રવેગ કેટલો હશે ?View Solution
- 2દળ $m $ અને ત્રિજ્યા $ r$ નો ઘન ગોળો ઢોળાવવાળા સમતલ પરથી રોલિંગ કરીને નીચે આવે છે ત્યારે ગતિઊર્જા....View Solution
- 3View Solutionઘનની જડત્વની ચાકમાત્રા કઈ અક્ષ પર ન્યૂનત્તમ છે ?
- 4એક ચકડોળ પ્રતિ મિનિટ $ 120 $ ભ્રમણો કરે છે. ચકડોળમાં બેસેલ એક બાળક રડતાં, ચકડોળને $ 2\ rad s^{-2}$ ના પ્રતિ પ્રવેગથી ધીમું પાડવામાં આવે છે, તો કેટલા સમયમાં ચકડોળ ઊભું રહેશે ? કેટલા પરિભ્રમણો બાદ ચકડોળ ઊભું રહેશે ?View Solution
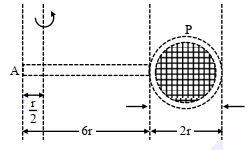
- 5આકૃતિમાં એક બેડમિન્ટન રેકેટના પરિમાણ આપેલા છે. જો બેડમિન્ટનના રેખીય અને વર્તુળાકાર ભાગનું સમાન દળ $(M)$ અને દોરીનું દળ અવગણ્ય હોય તો, હેન્ડલના બિંદુ $A$ થી $\frac{r}{2}$ અંતરે રેકેટના હેન્ડલને લંબ અને રિંગના સમતલમાં રહેલી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા ....... $Mr^2$ જેટલી થાય?View Solution
- 6View Solutionફ્લાય વ્હીલને એક એન્જિન સાથે વાપરવામાં આવે છે કારણ કે તે,
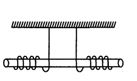
- 7$M $ દળ અને $R$ ત્રિજ્યાનો ઘન નળાકાર સમક્ષિતિજ સ્થિતિમાં મૂકેલો છે. બે દોરી નળાકારની ફરતે વીટાળેલી છે. જેમ દોરીના વળ ઉકલતા જાય તેમ દોરીમાં તણાવ અને નળાકારનો પ્રવેગ શોધો.View Solution
- 8$M $ દળ અને $R$ ત્રિજ્યાવાળો નક્કર નળાકાર $ L$ લંબાઈના ઢાળ પરથી સરક્યા સિવાય ગબડે છે. ઢાળની ઊચાઈ $h$ છે. જ્યારે નળાકાર ઢાળના તળિયે પહોંચે ત્યારે તેના દ્રવ્યમાન-કેન્દ્રનો વેગ કેટલો હશે ?View Solution
- 9$I$ જડત્વની ચાકમાત્રા ધરાવતા ચક્ર $1\ sec$ માં $n$ પરિભ્રમણ કરે છે.તેની આવૃત્તિ બમણી કરવા માટે કરવું પડતું કાર્યView Solution
- 10$ℓ$ લંબાઈનો બાજુનું માપ વાળા ચોરસના ચારેય ખૂણા પર $m$ દળના ચાર ગણો મૂકેલા છે. તેના કેન્દ્રમાંથી પસાર થતી અને ચોરસના સમતલને લંબ અક્ષ પર તંત્રની ચક્રાવર્તનની ત્રિજ્યા ......... છે.View Solution