$m _{1}$ અને $m _{2}$ દળનાં બે કણોનું બનેલું એક તંત્ર વિચારો. જો પ્રથમ કણને દ્રવ્યમાનકેન્દ્ર તરફ $d$ અંતર ખસેડવામાં આવે, તો બીજા કણને કેટલો ખસેડવો જોઈએ કે જેથી દ્રવ્યમાનકેન્દ્ર તે સમાન સ્થાને રહે?
AIEEE 2006,AIPMT 2004, Medium
d
Initially,
Initially,
\(0 = \frac{{{m_1}\left( { - {x_1}} \right) + {m_2}{x_2}}}{{{m_1} + {m_2}}} \Rightarrow {m_1}{x_1} = {m_2}{x_2}\,\,\,\,\,...\left( 1 \right)\)
Finally,
The centre of mass is at the origin
\(\therefore 0 = \frac{{{m_1}\left( {d - {x_1}} \right) + {m_2}\left( {{x_2} - d'} \right)}}{{{m_1} + {m_2}}}\)
\(\begin{array}{l}
\Rightarrow 0 = {m_1}d - {m_1}{x_1} + {m_2}{x_2} - {m_2}d'\\
\Rightarrow d' = \frac{{{m_1}}}{{{m_2}}}d\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,[Form\,\left( 1 \right).]
\end{array}\)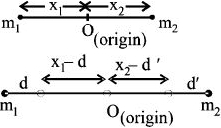
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચે દર્શાવેલ આકૃતિ મુજબ બળદગાડાનું પૈડુ એક લેવલ (સમથલ) રસ્તા ઉપર ગબડે છે. દર્શાવેલ દિશામાં જો તેની રેખીય ઝડપ $v$ હોય તો નીચેનામાંથી ક્યો વિકલ્પ સાચો છે? $(P$ અને $Q$ ક્રમશઃ પૈડાનું સૌથી ઉંચુ અને નીચુ બિંદુ દર્શાવે છે.)View Solution
- 2એક પાતળી ચોરસ તકતી જેનું દળ $m$ અને બાજુની લંબાઈ $a$ છે તેના વિકર્ણને અનુલક્ષીને જડત્વની ચાકમાત્રા $I$ હોય તો ...View Solution
- 3View Solutionપદાર્થ સમક્ષિતિજ સપાટી પર સરક્યા સિવાય રોલિંગ કરે છે. તેની ચાકગતિ ઊર્જાએ સ્થાનાંતરિત ગતિ ઊર્જા જેટલી છે. તો પદાર્થ ....... છે.
- 4અનુક્રમે $10\,kg$ અને $20\,kg$ દળ ધરાવતા બે વસ્તુઓને $10\,m$ લંબાઈ અને અવગણ્ય દળ ધરાવતા દઢ સળિયા વડે જોડવામાં આવેલા છે. $10\,kg$ દળથી દ્રવ્યમાન કેન્દ્રનું અંતર$.....$View Solution
- 5$I_1=4 \mathrm{~kg} \mathrm{~m}^2$ અને $I_2=2 \mathrm{~kg} \mathrm{~m}^2$ જેટલી જડત્વની ચાકમાત્રા ધરાવતી બે તકતી, તેઓની કેન્દ્રીય અક્ષો અને તક્તિઓન લંબ હોય તને અનુલક્ષીને અનુક્રમે $10 \mathrm{rad} / \mathrm{s}$ અને $4 \mathrm{rad} / \mathrm{s}$ ની કોણીય ઝડપથી ભ્રમણ કરે છે જેને તેઓની પરિભ્રમણ અક્ષો એકબીજા પર સંપાત થાય તે રીતે સામસામે એકબીજાના સંપર્કમાં લાવવામાં આવે છે. આ પ્રક્રિયા દરમ્યાન ગતિ ઊર્જામાં થતો ધટાડો__________$\mathrm{J}$છે.View Solution
- 6View Solutionએક પાતળી સમક્ષિતિજ તકતી તેના કેન્દ્રમાંથી પસાર થતી શિરોલંબ અક્ષને અનુલક્ષીને ચાકગતિ કરે છે. એક જંતુ એ તકતીના વ્યાસ પર એક છેડેથી સામેના બીજા છેડે ગતિ કરે છે. તો તેની ગતિ દરમિયાન તકતીની કોણીય ઝડપ.....
- 7$m=5$ નો કણ $v = 3\sqrt 2$ ના અચળ વેગથી $XOY$ સમતલમાં $Y = X + 4$ રેખા પર ગતિ કરે છે. તેનું ઉગમબિંદુને અનુલક્ષીને કોણીય વેગમાન કેટલું મળે?View Solution
- 8સમાન દળ અને જુદી-જુદી ત્રિજ્યાઓ ધરાવતી બે તક્તિઓ કે જે જુદા-જુદા દ્રવ્યોની બનેલી છે તે એવી રીતે બનાવવામાં આવે છે કે જેથી તેની જાડાઈ અનુક્રમે $1\,cm$ અને $0.5\,cm$ હોય. દ્રવ્યની ઘનતાઓ $3:5$ ના ગુણોતરમાં છે. આ તક્તિઓની તેમનાં વ્યાસને અનુલક્ષીને જડત્વની ચાક્માત્રાઓ $\frac{x}{6}$ નાં ગુણોતરમાં મળે છે. $x$ નું મૂલ્ય $........$ થશે.View Solution
- 9સમાન દળ અને જુદી-જુદી ત્રિજ્યાઓ ધરાવતી બે તક્તિઓ કે જે જુદા-જુદા દ્રવ્યોની બનેલી છે તે એવી રીતે બનાવવામાં આવે છે કે જેથી તેની જાડાઈ અનુક્રમે $1\,cm$ અને $0.5\,cm$ હોય. દ્રવ્યની ઘનતાઓ $3:5$ ના ગુણોતરમાં છે. આ તક્તિઓની તેમનાં વ્યાસને અનુલક્ષીને જડત્વની ચાક્માત્રાઓ $\frac{x}{6}$ નાં ગુણોતરમાં મળે છે. $x$ નું મૂલ્ય $........$ થશે.View Solution
- 10$1\ kg $ અને $3\ kg$ આંતરિક બળોના કારણે એકબીજા તરફ ગતિ કરે છે.જયારે તેમનો સાપેક્ષ વેગ $2\ m/s$ હોય,ત્યારે દ્રવ્યમાન કેન્દ્ર નો વેગ $0.5\ m/s$ છે.તો જયારે તેમનો સાપેક્ષ વેગ $3\ m/s$ હોય,ત્યારે દ્રવ્યમાન કેન્દ્ર નો વેગ ......... $m/s$ થાય.View Solution
