\(f =\mu (M + m) g\)
\(\begin{gathered}
a = \frac{f}{{M + m}} = \frac{{\mu \left( {M + m} \right)g}}{{(M + m)}} = \mu g \hfill \\
= 0.05 \times 10 = 0.5\,m{s^{ - 2}} \hfill \\
{V_0} = \frac{{Initial\,momentum\,}}{{\left( {M + m} \right)}} = \frac{{0.05V}}{{10.05}} \hfill \\
m = 50g\,\,\,\,\,\,\,\,\,\,\,\,M = 10\,kg \hfill \\
\end{gathered} \)
\({\left( {\frac{{0.05v}}{{10.05}}} \right)^2} = 2 \times 0.5 \times 2\)
Solving we get \(v = 201\sqrt 2 \) object falling from height \(H.\)
\(\begin{gathered}
\frac{V}{{10}} = \sqrt {2gh} \hfill \\
\frac{{201\sqrt 2 }}{{10}} = \sqrt {2 \times 10 \times H} \hfill \\
\end{gathered} \)
\(H = 40\; m = 0.04\; km\)
\(\begin{gathered}
{v^2} - {u^2} = 2as \hfill \\
0 - {u^2} = 2as \hfill \\
{u^2} = 2as \hfill \\
\end{gathered} \)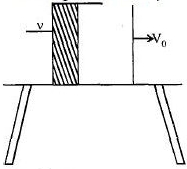
Download our appand get started for free
Similar Questions
- 1બળ $\vec{F}=(2+3 x) \hat{i}$ એ એક કણ ઉપર $x$ દિશામાં પ્રવર્તે છે, જ્યાં $F$ એ ન્યૂટનમાં અને $x$ મીટરમાં છે. $x=0$ થી $x=4\,m$ ના સ્થાનાંતર દરમ્યાન આ બળ દ્વારા થતું કાર્ય .....$J$ હશે.View Solution
- 2View Solutionએક બોલ ભોયતળિયે અથડાઈને પાછો ફરે છે. તો આ સ્થિતિ સ્થાપક અથડામણના કિસ્સા માટે......
- 3$1.6\, m$ લાંબી દોરી સાથે બાંધેલી ટોપલી ને શિરોલંબ દિશામાં વર્તુળાકારે અચળ ઝડપથી ભ્રમણ કરાવવામાં આવે છે. તો જ્યારે ટોપલી ઉચ્ચત્તમ સ્થાને હોય ત્યારે તેમાથી પાણી ન ઢોળાય તે માટે તેની ન્યુનત્તમ ઝડપ ........ $m/sec$ હોવી જોઇયે.View Solution
- 4દ્વિ-પરમાણ્વીય અણુ માટે સ્થિતિ ઊર્જ $(U)$ આંતર આણ્વીય અંતર $r$ નું વિધેય છે, કે જેView Solution
$U =\frac{\alpha}{ r ^{10}}-\frac{\beta}{ r ^{5}}-3$
જ્યાં,$\alpha$ અને $\beta$ ધન અચળાંકો છે. બે પરમાણુઓ વચ્ચેનું સંતુલન અંતર $\left(\frac{2 \alpha}{\beta}\right)^{\frac{a}{b}}$ હશે જ્યાં $a=..........$ છે
- 5એક $m$ દળનો પદાર્થ $r$ ત્રિજ્યાના વર્તૂળમાં $V$ જેટલી સમાન ઝડપથી ગતિ કરે છે. $m V^2/r$ જેટલું બળ પદાર્થના કેન્દ્ર પર સીધું જ લાગે છે. આ બળ દ્વારા જ્યારે પદાર્થ વર્તૂળના પરિઘનું અડધું અંતર કાપે તે દરમિયાન પદાર્થ દ્વારા થતું કાર્ય શોધો.View Solution
- 6$m$ દળનો $v$ વેગથી ગતિ કરતો કણ, $2m$ દળવાળા સ્થિર કણ સાથે સંધાત અનુભવે છે. સંધાત બાદ તેઓ એકબીજા સાથે ચોંટી જાય છે અને ગતિ ચાલુ રાખે છે, તો તેમનો વેગ ......... થાય.View Solution
- 7એક માણસની ગતિઊર્જા તેનાથી અડઘું દળ ઘરાવતા છોકરાથી અડઘી છે.જો માણસની ઝડપમાં $ 1 m/s$ નો વઘારો કરવામાં આવે તો બંનેની ગતિઊર્જા સમાન થાય છે. માણસની મૂળ ઝડપView Solution
- 8બે સમાન ગોળાઓ $A$ અને $B$ અનુક્રમે $0.5 \;m/s$ તથા $ -0.3 \;m/s $ ના વેગથી એક પરિમાણમાં ગતિ કરતાં સ્થિતિસ્થાપક અથડામણ અનુભવે છે. અથડામણ પછી ગોળા $ B$ અને ગોળા $A$ ના વેગ અનુક્રમે કેટલા થાય?View Solution
- 9$100\; g$ દળનો એક કણ શિરોલંબ દિશામાં ઉપર તરફ $5\;m/s$ નાં વગેથી ફેકવામાં આવે છે. તો કણ જ્યારે ઉપર પહોંચે ત્યારે તે સમયમાં ગુરુત્વાકર્ષણ બળ વડે થયેલું કાર્ય ($J$ માં) કેટલું હશે?View Solution
- 10$X- $ અક્ષની દિશામાં ગતિ કરવા માટે મુકત એવા $1\; kg $ દળના પદાર્થ માટે સ્થિતિ-ઊર્જા નીચેના સૂત્રથી મળે છે: $U\left( x \right) = \left( {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right)$ $J $ તેની યાંત્રિક ઊર્જા $2\;J $ છે,તો તેની મહત્તમ ઝડપ $m/s$ માં કેટલી થાય?View Solution
