$m , 2 m , 4 m$ અને $8 m$ દળના બ્લોકને ઘર્ષણરહિત સપાટી પર મુકેલ છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે બીજો $m$ દળનો બ્લોક તે જ રેખા પર $v$ વેગથી ગતિ કરીને $m$ દળના બ્લોક સાથે સંપૂર્ણ અસ્થિતિસ્થાપક સંઘાત અનુભવે છે. બિજા બધા પછીના સંઘાત સંપૂર્ણ અસ્થિતિસ્થાપક સંઘાત છે. જે સમયે $8m$ દળનો બ્લોક ગતિ કરવાનું શરૂ કરે ત્યારે તેની શરૂઆતની કુલ ઉર્જા ની $p \%$ ઉર્જાનો વ્યય થાય છે. તો $p$ નું મૂલ્ય લગભગ કેટલું હશે?
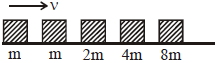

JEE MAIN 2020, Diffcult
d
All collisions are perfectly inelastic, so affer the final collision, all blocks are moving together. So let the final velocity be \(v^{\prime},\) so on applying momentum conservation:
All collisions are perfectly inelastic, so affer the final collision, all blocks are moving together. So let the final velocity be \(v^{\prime},\) so on applying momentum conservation:
\(mv =16 m v ^{\prime} \Rightarrow v ^{\prime}= v / 16\)
Now initial energy \(E _{1}=\frac{1}{2} mv ^{2}\)
Final energy \(: E _{ f }=\frac{1}{2} \times 16 m \times\left(\frac{ v }{16}\right)^{2}\)
\(\Rightarrow E _{ f }=\frac{1}{2} m \frac{ v ^{2}}{16}\)
Energy loss : \(E _{ i }- E _{ f }\)
\(\Rightarrow \frac{1}{2} mv ^{2}-\frac{1}{2} m \frac{ v ^{2}}{16}\)
\(\Rightarrow \frac{1}{2} mv ^{2}\left[1-\frac{1}{16}\right] \Rightarrow \frac{1}{2} mv ^{2}\left[\frac{15}{16}\right]\)
\(\% p=\frac{\text { Energy loss }}{\text { Original energy }} \times 100\)
\(=\frac{\frac{1}{2} mv ^{2}\left[\frac{15}{16}\right]}{\frac{1}{2} mv ^{2}} \times 100=93.75 \%\)
\(\Rightarrow\) Value of \(P\) is close to \(94\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ટ્રક $1200 kg$ નું દળ ઉંચકીને સમતલ રસ્તા પર $10m/s $ ની સ્થાયી ઝડપથી ગતિ કરે છે. જોડાણ વચ્ચેનું તણાવ $1000 N $ છે. દળ પર વપરાતો પાવર ..... હશે. જ્યારે ટ્રક રસ્તા પરના $1m$ ઢાળ અને $6$ મી. ઉંચાઈ વાળા સમતલ પર ગતિ કરે ત્યારે તણાવ ..... હશે.View Solution
- 2View Solutionપદાર્થ પર લાગતું બળ એ તેની ઝડપના વ્યસ્ત પ્રમાણમાં હોય તો પદાર્થની ગતિ ઊર્જા કેવી હશે?
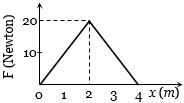
- 3$25 kg$ નો પદાર્થનો બળ વિરુધ્ધ સ્થાનાંતરનો આલેખ આપેલ છે.પદાર્થનો શરૂઆતનો વેગ $ 2 m/s$ હોય,તો $4 m$ અંતર કાપ્યા પછી તેની ગતિઊર્જા કેટલા .............. $\mathrm{J}$ થશે?View Solution
- 4$X$ દિશામાં એક કણ પર $F = (10 + 0.5x) \;N$ બળ લાગે છે. જ્યાં $x$ મીટરમાં છે. $x = 0$ થી $x = 2$ સુધીના સ્થાનાંતર દરમિયાન આ બળ દ્વારા થતું કાર્ય શોધો.View Solution
- 5સંપૂર્ણ સ્થિતિસ્થાપક સંધાત માટે રેસ્ટીંટયુશન ગુણાંક $e$ કેટલો હોય છે?View Solution
- 6પશ્રિમ દિશા તરફ $v$ વેગથી ગતિ કરી રહેલાં $m$ દળનો એક કણ સાથે અથડામણ અનુભવે છે. જો બંને કણો એેકબીજા સાથે ચોંટી જાય તો, $2 m$ દળ વાળા નવા કણની ઝડપ ......... હશે.View Solution
- 7$m $ દળ અને $ v$ વેગની એક ગોળી $M$ દળના લોલક આગળથી પસાર થાય છે અને $v/2$ વેગ સાથે અથડાય છે. $v$ ની કઈ ન્યૂનત્તમ કિંમત માટે લોલક સંપૂર્ણ ચક્ર પૂર્ણ કરશે ?View Solution
- 8$100m$ ઊંચાઇ ધરાવતી ટેકરી પર $20 kg$ નો ગોળો ગતિ કરીને જમીન પર આવીને $30m$ ઊંચાઇ ધરાવતી બીજી ટેકરી પર અને ત્યાંથી $20m$ ઊંચાઇ ધરાવતી ત્રીજી ટેકરી પર આવતાં તેનો વેગ કેટલા .............. $\mathrm{m} / \mathrm{s}$ થશે?View Solution
- 9પ્રારંભમાં સ્થિર પદાર્થ $2M $ અને $3M $ દળ ના બે ટૂકડામાં વહેંચાય છે અને તેમની બંનેની મળીને કુલ ગતિઊર્જા $E$ છે. ટૂકડામાં વહેંચાયા બાદ $ 2M$ દળના ટૂકડાની ગતિઊર્જા કેટલી હશે?View Solution
- 10$4 \,m$ ઊંચી ઢોળાવવાળી સપાટી પર $5 \,kg$ દળ ધરાવતાં બ્લોકને ઉપર તરફ ખસેડવા માટે $250 \,J$ જેટલું કાર્ય થયું હોય તો, ઘર્ષણ વિરુદ્ધ થયેલ કાર્યનું મૂલ્ય .......... $J$ છે. $\left(g=10 \,ms ^{-2}\right)$View Solution
