$m$ અને $4 \,m$ દળનાં બે બિંદુવતૂ દળો એ એક રેખા પર $d$ અંતરે મૂકલલા છે. જો ત્રીજા $m_0$ દળના બિંદુવત દળને રેખા પર એવી રીતે મૂકવામાં આવે છે કે તેના પરનું પરિણામી ગુરુત્વાકર્ષણ બળ શૂન્ય છે. $m$ દળથી તે બિંદુનું અંતર ............. છે ?
Medium
Download our app for free and get started
c
(c)
(c)
Force of gravitation on \(m_0\) due to \(m=\frac{G m m_0}{r^2}=F_1\)
Force of gravitation on \(m_0\) due to \(4 m=\frac{G 4 m m_0}{(d-r)^2}=F_2\)
Net force \(=0\)
\(\Rightarrow F_1=F_2\)
\(\frac{G m m_0}{r^2}=\frac{4 G m m_0}{(d-r)^2}\)
\(\Rightarrow (d-r)^2=(2 r)^2\)
\(\Rightarrow d-r=2 r\)
\(\Rightarrow d=3 r\)
Thus, \(r=\frac{d}{3}\)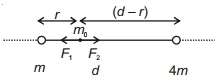
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પૃથ્વીની સપાટીની નજીક ભ્રમણ કરતાં ઉપગ્રહનો કક્ષીય વેગ $v$ છે,તો પૃથ્વીની સપાટીથી પૃથ્વીની ત્રિજયા કરતાં અડધી ઊંચાઇ ધરાવતી કક્ષામાં ભ્રમણ કરતાં ઉપગ્રહનો કક્ષીય વેગ કેટલો થાય?View Solution
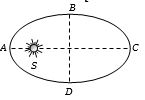
- 2View Solutionએક ગ્રહ સૂર્યની ફરતે નીચે મુજબ ગતિ કરે છે. તો ગ્રહનો કક્ષીય વેગ ન્યૂનતમ ક્યાં હશે ?
- 3એક પદાર્થ $M$ દળ અને $R$ ત્રિજ્યા ધરાવતા ગ્રહની ફરતે નીચી વર્તુળાકાર કક્ષામાં ગતિ કરે છે. તેની કક્ષાની ત્રિજ્યાને $R$ પણ લઈ શકાય. તો આ પદાર્થના કક્ષીય વેગ અને આ ગ્રહની નિષ્ક્રમણ ઝડપનો ગુણોત્તર કેટલો થાય?View Solution
- 4સૂર્યથી ઉલ્કાપિંડનું મહત્તમ અને લઘુતમ અંતર $1.6 \times 10^{12}\, m$ અને $8.0 \times 10^{10}\, m$ છે. સૂર્યથી નજીકના બિંદુએ ઉલ્કાપિંડનો વેગ $6 \times 10^{4}\, ms ^{-1}$ હોય તો સૂર્યથી દૂરના બિંદુએ ઉલ્કાપિંડનો વેગ .............. $\times 10^{3}\, m / s$ હશે.View Solution
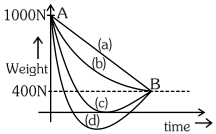
- 5$100\, {kg}$ દળ ધરાવતો વ્યક્તિ સ્પેસશીપમાં પૃથ્વીથી મંગળ સુધી મુસાફરી કરે છે. આકાશમાંના અન્ય તમામ પદાર્થોને અવગણો અને પૃથ્વી અને મંગળની સપાટી પર ગુરુત્વપ્રવેગ અનુક્રમે $10\;{m} / {s}^{2}$ અને $4 \,{m} / {s}^{2}$ છે. નીચે આપેલા ગ્રાફમાંથી ક્યો વક્ર મુસાફરના વજનનો સમયના વિધેય સાથેનો શ્રેષ્ઠ ફેરફાર દર્શાવે છે.View Solution
- 6View Solutionજ્યાં ગુરુત્વાકર્ષી ક્ષેત્ર શૂન્ય હોય ત્યાં ગુરુત્વસ્થિતિમાન
- 7પૃથ્વીની ફરતે ભ્રમણ કરતાં ઉપગ્રહ નો નિષ્ક્રમણ વેગ $({V_e })$ તેના પરિભ્રમણ વેગ $({V_o })$, કરતાં કેટલા ગણો થાય ?View Solution
- 8View Solutionનીચેના પૈકી ઉપગ્રહ માટે શું ખોટું છે ?
- 9બે પદાર્થ જેનું દળ $m_1$ અને $m_2$ છે તે અનંત અંતરે સ્થિર પડેલા છે. હવે તે બંને એકબીજા તરફ ગુરુત્વાકર્ષણ બળને લીધે ગતિ કરે છે. જ્યારે તે બંને એકબીજાથી $r$ અંતરે આવે ત્યારે તેનો સાપેક્ષ વેગ કેટલો થાય ?View Solution
- 10View Solutionજો પૃથ્વીનો કોણીય વેગ એવી રીતે વધારવામાં આવે કે જેથી પૃથ્વીના વિષુવવૃત પર પદાર્થ તરવા લાગે તે રીતે પૃથ્વી ભ્રમણ કરે છે તો પૃથ્વીના આવર્તકાળ (મિનિટમાં) શું હશે