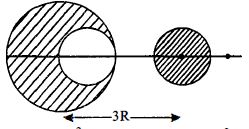
$M$ દળ અને $R$ ત્રિજ્યા ધરાવતા ગોળમાંથી $\frac{R}{2}$ ત્રિજ્યા ધરાવતો ગોળો કાપીને આકૃતિમાં દર્શાવ્યા પ્રમાણે મૂકેલા છે.જેમાં બંને ગોળાના કેન્દ્ર વચ્ચેનું અંતર $3R$ છે.તો બંને ગોળા વચ્ચે લાગતું ગુરુત્વાકર્ષણ બળ કેટલું હશે?

JEE MAIN 2014, Diffcult
a
Volume of removed sphere
Volume of removed sphere
\({V_{remo}} = \frac{4}{3}\pi {\left( {\frac{R}{2}} \right)^3} = \frac{4}{3}\pi {R^3}\left( {\frac{1}{8}} \right)\)
Volume of the sphere (remaining)
\({V_{remain}} = \frac{4}{3}\pi {R^3} - \frac{4}{3}\pi {R^3}\left( {\frac{1}{8}} \right)\)
\( = \frac{4}{3}\pi {R^3}\left( {\frac{7}{8}} \right)\)
Therefore mass of sphere carved and remaining sphere are at respectively \(\frac{1}{8}\,M\,and\,\frac{7}{8}\,M.\)
Therefore, gravitational force between these two sphere
\(F = \frac{{GMm}}{{{r^2}}}\)
\( = \frac{{G\frac{{7M}}{8} \times \frac{1}{8}M}}{{{{\left( {3R} \right)}^2}}} = \frac{7}{{64 \times 9}}\frac{{G{M^2}}}{{{R^2}}}\)
\( = \frac{{41}}{{3600}}\frac{{G{M^2}}}{{{R^2}}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઉપગ્રહનો કક્ષીય આવર્તકાળ $T$ હોય,તો તેની ગતિઊર્જા કોના સપ્રમાણમાં હોય?View Solution
- 2પૃથ્વી કેટલી કોણીય વેગ થી ફરવી જોઈએ કે $60^o$ અક્ષાંશ પર તેનો ગુરુત્વ પ્રવેગ શૂન્ય થાય?View Solution
- 3ચંદ્ર પર ગુરુત્વ પ્રવેગ પૃથ્વી પરના ગુરુત્વ પ્રવેગ કરતાં $\frac 16$ ગણું છે. જો તેમની ઘનતા નો ગુણોત્તર પૃથ્વી $({\rho _e})$અને ચંદ્ર $\left( {\frac{{{\rho _e}}}{{{\rho _m}}}} \right) = \frac{5}{3}$ છે તો $R_m$ ને $R_e$ ના સ્વરૂપ માં કઈ રીતે લખાય ?View Solution
- 4સ્ટીલના અને લાકડાના દડાને $h$ ઊંચાઈ થી શૂન્યાવકાશ માથી મુક્ત કરવામાં આવે તો બંને ને જમીન પહોચવા લાગતો સમય સરખો હોય તે માટેનું કારણView Solution
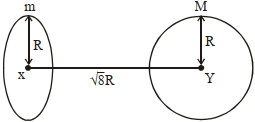
- 5આકૃતિમાં દર્શાવેલ ગોળા અને વલય (રીંગ) વચ્ચે આકર્ષણ બળ શોધો, જ્યાં રીંગનું સમતલ કેન્દ્રોને જોડતી રેખાને લંબરૂપે છે. બે રિંગ $('m'$ દળ) નાં કેન્દ્ર થી ગોળા $('M'$ દળ)નાં કેન્દ્ર વચ્ચેનું અંતર $\sqrt{8} R$ હોય તેમજ બંને એકસરખી ત્રિજ્યા $'R’$ ધરાવે છે.View Solution
- 6પૃથ્વીની ત્રિજયા $6400\, km$ અને ગુરુત્વપ્રવેગ $g = 10\,m/{\sec ^2}$ હોય,તો $5\, kg$ ના પદાર્થને વિષુવવૃત્ત પાસે વજનરહિત કરવા માટે પૃથ્વીની કોણીય ઝડપ કેટલી કરવી જોઈએ?View Solution
- 7પૃથ્વીની સપાટીથી (પૃથ્વીની ત્રિજ્યા $6.4 \times 10^3 \,km$) $h$ ઊંચાઈ પર એક ઉપગ્રહને રાખવા માટેની જરૂરી ઊર્જા $E_1$ છે અને આ ઉપગ્રહને આ ઊંચાઈ પર વર્તુળાકાર કક્ષામાં રાખવા જરૂરી ગતિ ઊર્જા $E_2$ છે. $E_1$ અને $E_2$ સમાન થાય તેવી ઊંચાઈ $h$ નું મૂલ્ય છેView Solution
- 8$m$ દળના પદાર્થને પૃથ્વીની સપાટી પર મૂકેલો છે. તેને પૃથ્વીની સપાટીથી $h = 3R$ ઊંચાઇ પર લઈ જવામાં આવે છે. પદાર્થની ગુરુત્વ સ્થિતિઊર્જામાં થતો ફેરફાર કેટલો હશે?View Solution
- 9બે $M$ અને $16\, M$ દળ ધરાવતા ગ્રહની ત્રિજ્યા અનુક્રમે $a$ અને $2\, a $ છે. બંને ગ્રહના કેન્દ્ર વચ્ચેનું અંતર $10\, a$ છે. $m$ દળના પદાર્થને મોટા ગ્રહ પરથી બંને ગ્રહના કેન્દ્રને જોડતી રેખા પર નાના ગ્રહ તરફ ફેકવામાં આવે છે. પદાર્થ નાના ગ્રહની સપાટી પર પહોચે તેના માટે તેને લઘુતમ કેટલી ઝડપથી ફેકવો જોઈએ?View Solution
- 10$m$ દળના કણો $A$ અને $B$ ના મધ્યબિંદુ પર મુકવામાં આવે છે. તો $C$ ને બિંદુ $A$ અને $B$ થી સમાન અંતર $r$ પર પ્રવેગ વગર લઈ જવા માટે થયેલ કાર્ય શોધો. ( $G=$ ગુરુત્વાકર્ષણ અચળાંક અને માત્ર $A, B$ અને $C$ વચ્ચેની ગુરૂત્વાકર્ષણ આંતરક્રિયા ધ્યાનમાં લેવામાં આવે છે.)View Solution
