$M$ દળ અને $r$ ત્રિજયા ધરાવતા નળાકાર પર $m$ દળ લટકાવતા તેનો પ્રવેગ
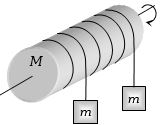
Diffcult
Download our app for free and get started
b
Tension in the both string will be same.
Tension in the both string will be same.
\(m g-T=m a....(1)\)
also Inertia solid cylinder is \(M R^{2} / 2\) Torque at centre of cylinder due to both string \(2 T \times R=I \alpha=M R^{2} \alpha / 2 \ldots(2)\)
also, \(a=\alpha R....(3)\)
From equations \((1),(2)\) and \((3)\)
we get Tension \(T=\frac{M m g}{M+4 m}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1દળ બદલ્યા સિવાય પૃથ્વીની ત્રિજ્યા અત્યારે તેની ત્રિજ્યા છે તેના કરતા ઘટાડીને ત્રણ-ચર્તુથાંશ જેટલી કરવામાં આવે તો પૃથ્વી પરના દિવસનો ગાળો. . . . . કલાક $30$ મિનિટ થશે.View Solution
- 2$M$ દળ ધરાવતો પદાર્થ $A$ ગુરુત્વાકર્ષણ બળની અસર હેઠળ પડતાં તે બે ટુકડાઓમાં વિભાજિત થાય છે. એક ટુકડો $B$ નું દળ $1/3\ M$ અને બીજા ટુકડા $ C$ નું દળ $ 2/3\ M$ છે. પદાર્થ $A$ ના દ્રવ્યમાન કેન્દ્રની સાપેક્ષે ટુકડાઓ $ B$ અને $ C$ થી બનતાં તંત્રનું દ્રવ્યમાન-કેન્દ્ર .....View Solution
- 3$10\ kg$ દળ અને $ 0.4\ m$ વ્યાસ ધરાવતી રિંગ તેની અક્ષની આસપાસ ભ્રમણ કરે છે. જો તે $ 2100$ પરીભ્રમણ દર મિનિટે કરે તો તેમનો કોણીય વેગમાન ....... $kg - m^2/s$ હોય?View Solution
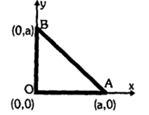
- 4View Solutionત્રણ સમાન દળના સળિયા આકૃતિમાં દર્શાવેલ છે. તંત્રના દ્રવ્યમાન કેન્દ્રના યામાક્ષ બિંદુઓ શોધો.
- 5એક પદાર્થ એક સ્થિર અક્ષને અનુલક્ષીને $3 \,rad / s ^2$ ના કોણીય પ્રવેગ સાથે ભ્રમણ કરે છે. જે સમયે તેનો કોણીય વેગ $10 \,rad / s$ માંથી. વધી ને $20 \,rad / s$ થાય તે સમય દરમિયાન તેના દ્વારા ભ્રમણ કરવામાં આવેલો કોણ ($rad$ માં) શું થાય?View Solution
- 6$5 \,kg$ અને $2 \,kg$ દળો ધરાવતા બે બ્લોક ને એક અવગણ્ય દળ ધરાવતી સ્પ્રિગ વડે જોડવામાં આવે છે અને તેને એક ધર્ષણ રહિત સમક્ષિતિજ સપાટી પર મૂકવામાં આવે છે. આઘાતએે ભારે બ્લોકને હલકાં બ્લોકની દિશામાં $7 \,m / s$ નો વેગ આપે છે. તો દ્રવ્યમાન કેન્દ્ર નો વેગ ......... $m / s$ થાય?View Solution
- 7$M $ દળ અને $L$ લંબાઈ ધરાવતા એક સળિયા $PQ$ નો $P$ છેડો જડિત કરેલ છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે, દળ રહિત દોરી વડે બિંદુ $Q$ સાથે બાંધીને આ સળિયાને સમક્ષિતિજ રાખવામાં આવેલ છે. જયારે દોરીને કાપી નાખવામાં આવે, ત્યારે સળિયાનો પ્રારંભિક કોણીય પ્રવેગ કેટલો થશે?View Solution
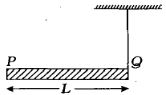
- 8$72\, km/h$ ની ઝડપથી જતી કારને બ્રેક મારતાં ટાયર $20$ પરિભ્રમણ પછી સ્થિર થાય છે.જો ટાયરનો વ્યાસ $0.5\, m$ હોય,તો કોણીય પ્રતિપ્રવેગ ($rad/s^2$ માં) કેટલો થાય?View Solution
- 9$2\ kg$ દળ અને $ 0.2\ m$ ત્રિજ્યાનો ઘન નળાકાર $3\ rad/sec$ ના કોણીય વેગથી ચાકગતિ કરે છે $0.5\ kg$ દળનો કણ $5\ ms^{-1} $ ના વેગથી ગતિ કરતા તેના પરિઘ પર અથડાય છે અને ચોટી જાય છે તો અથડામણના લીધે ગતિઊર્જામાં ....... $J$ ઊર્જાનો વ્યય થાય છે.View Solution
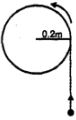
- 10ઘન તકતીનો વ્યાસ $ 0.5\ m $ અને તેનું દળ $16\ kg$ છે $8 $ સેકન્ડમાં કોણીય વેગ શૂન્યથી $120$ ભ્રમણ/ મિનિટ વધારવા માટે કેટલું ટોર્ક આપવું જોઈએ ?View Solution