$M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતીની કોણીય ઝડપ $\omega_{1}$ છે. બીજી $\frac{ R }{2}$ ત્રિજ્યા અને $M$ દળ ધરાવતી તકતી તેના પર મુક્તા નવી કોણીય ઝડપ $\omega_{2}$ છે.શરૂઆતની ઊર્જાનો વ્યય થાય તો $p=.......$
JEE MAIN 2020, Diffcult
c
Let moment of inertia of bigger disc is \(I =\frac{ MR ^{2}}{2}\)
Let moment of inertia of bigger disc is \(I =\frac{ MR ^{2}}{2}\)
\(\Rightarrow\) \(MOI\) of small disc \(I_{2}=\frac{M\left(\frac{R}{2}\right)^{2}}{2}=\frac{I}{4}\)
by angular momentum conservation
\(I \omega_{1}+\frac{ I }{4}( D )= I \omega_{2}+\frac{ I }{4} \omega_{2} \Rightarrow \omega_{2}=\frac{4 \omega_{1}}{5}\)
initial kinetic energy \(K _{1}=\frac{1}{2} I \omega_{1}^{2}\)
final kinetic energy \(K _{2}\)
\(=\frac{1}{2}\left( I +\frac{ I }{4}\right)\left(\frac{4 \omega_{1}}{5}\right)^{2}=\frac{1}{2} I \omega_{1}^{2}\left(\frac{4}{5}\right)\)
\(P \%=\frac{ K _{1}- K _{2}}{ K _{1}} \times 100 \%=\frac{1-4 / 5}{1} \times 100=20 \%\)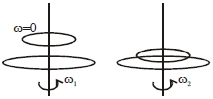
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પાતળા નિયમિત વર્તુળાકાર તક્તીનું દળ $m$ અને ત્રિજ્યા $R$ છે તે તેના મધ્યમાંથી પસાર થતી $axis$ અને તેના સમતલને લંબ એવા સમતલમાં ફરે છે. તેનો કોણીય વેગ $w$ છે. તેટલા જ દળની પણ તેનાથી અડધી ત્રિજ્યા ધરાવતી બીજી તકતી તેના પર સહજ રીતે મૂકવામાં આવે છે. આ સંયોજત તકતીનો કોણીય વેગ $..........$View Solution
- 2દળમાં ફેરફાર વગર જો પૃથ્વીની ત્રિજ્યા તેના વર્તમાન મૂલ્ય કરતાં $n$ ગણી થઈ જાય તો દિવસનો સમયગાળો કેટલો છે ?View Solution
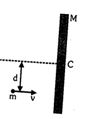
- 3$L$ લંબાઈ અને $M$ દળની લાકડી ઘર્ષણ રહિત સપાટી પર કોઇ પણ રીતે મુક્ત પણે ગતિ કરી શકે છે. $ m$ દળનો બોલ $ v$ ઝડપથી આકૃતિમાં દર્શાવ્યા પ્રમાણે ગતિ કરે છે. બોલનું દળ કેટલું હોવું જોઈએ કે જેથી અથડામણ બાદ તે સ્થિર રહે ?View Solution
- 4$50\,cm$ લાંબી એક નળીમાં $250\,g$ દળ ધરાવતું અદબનીય પ્રવાહી ભરેલું છે અને તે બંને છેડાઓથી બંધ કરેલ છે. ત્યારબાદ નળીને તેના એક છેડાને ફરતે સમક્ષિતિજ સમતલમાં $x \sqrt{F} \;rad s ^{-1}$ જેટલા નિયમિત કોણીયવેગથી ભ્રમણ કરાવવામાં આવે છે. જો $F$ એ પ્રવાહી દ્વારા બીજા છેડા પર લાગતું બળ હોય તો $x$ નું મૂલ્ય થશે.View Solution
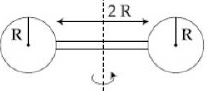
- 5$2R$ લંબાઇના અને $M$ દ્રવ્યમાનના એક સળીયાના બે છેડા પર $M$ દ્રવ્યમાન અને $R$ ત્રિજ્યાના બે સમાન ગોલીય બોલ લગાડેલ છે (આકૃતિ જુઓ). આ સળીયાની મધ્યમાંથી લંબરૂપે પસાર થતી અક્ષને સાપેક્ષે આ તંત્રની જડત્વની ચાકમાત્રા_____ થાય.View Solution
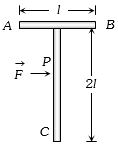
- 6આકૃતિમાં દર્શાવ્યા મુજબ $ T $ આકારનો પદાર્થ લીસી સપાટી પર છે. હવે બિંદુ $ P $ પર,$ AB $ ને સમાંતર દિશામાં બળ $\mathop F\limits^ \to $ એવી રીતે લગાવવામાં આવે છે, જેથી પદાર્થ ચાકગતિ કર્યા વિના ફક્ત રેખીય ગતિ કરે, તો બિંદુ $ C$ ની સાપેક્ષે બિંદુ $P$ નું સ્થાન શોધો.View Solution
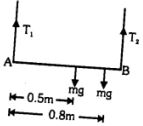
- 7આકૃતિમાં દર્શાવ્યા પ્રમાણે $ m$ દળની નિયમિત મીટરપટ્ટીનો છેડે બે શિરોલંબ દોરી વડે લટકાવેલી છે. $m$ દળનો પદાર્થ $80$ ના કાપાં પર મૂકેલો છે. તો દોરીમાં ઉદભવતા તણાવબળનો ગુણોત્તર શોધો.View Solution
- 8$M$ દળ, $L$ લંબાઈ અને $R$ ત્રિજ્યા ધરાવતા નળાકારના કેન્દ્રમાંથી અને નળાકારની અક્ષને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I = M \left(\frac{ R ^{2}}{4}+\frac{ L ^{2}}{12}\right) $ મુજબ આપવામાં આવે છે. જો આ નળાકારને એક એવા દ્રવ્યમાંથી બનાવવામાં આવે કે જેથી તેના માટે $I$ ન્યૂનતમ રાખવા માટે $\frac LR$ નો ગુણોત્તર કેટલો હોવો જોઈએ?View Solution
- 9$500\ gm$ દળ અને $10\ cm$ ત્રિજયા ધરાવતો ઘન ગોળો $20\ cm/s$ ના વેગથી ગબડે છે.તો કુલ ગતિઉર્જા ........ $J$View Solution
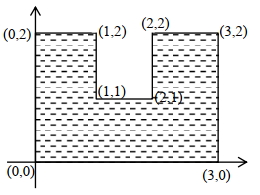
- 10આક્રુતિમાં દર્શાવ્યા અનુસાર $10 \mathrm{~kg}$ દળ ધરાવતી અને દર્શાવેલ પરિમાણ ધરાવતી એક નિયમીત પાતળી ધાત્વીય પ્લેટ (તક્તિ) દર્શાવેલ છે. જો તક્તિના દ્રવ્યમાન કેન્દ્રની $x$ યામ અને $\mathrm{y}$ ની ગુણોત્તર $\frac{n}{9}$ છે.$n$ નું મૂલ્ય. . . . . .થશે.View Solution