Total energy of satellite at height \(h\) from the earth surface,
\(E=PE+KE\)
\( = - \frac{{GMm}}{{\left( {R + h} \right)}} + \frac{1}{2}m{v^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\)
Also, \(\frac{{m{v^2}}}{{\left( {R + h} \right)}} = \frac{{GMm}}{{\left( {R + {h^2}} \right)}}\)
or, \({v^2} = \frac{{GM}}{{R + h}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)\)
From eqns, \((i)\) and \((ii)\),
\(E = - \frac{{GMm}}{{\left( {R + h} \right)}} + \frac{1}{2}\frac{{GMm}}{{\left( {R + h} \right)}} = - \frac{1}{2}\frac{{GMm}}{{\left( {R + h} \right)}}\)
\( = - \frac{1}{2}\frac{{GM}}{{{R^2}}} \times \frac{{m{R^2}}}{{\left( {R + h} \right)}}\)
\( = - \frac{{m{g_0}{R^2}}}{{2\left( {R + h} \right)}}\,\,\,\,\,\,\,\,\,\,\,\,\left( {{g_0} = \frac{{GM}}{{{R^2}}}} \right)\)
Download our appand get started for free
Similar Questions
- 1પૃથ્વીની આસપાસ વર્તુળાકાર કક્ષામાં ઉપગ્રહ અચળ ઝડપ $v$ થી ભ્રમણ કરે છે.જો પૃથ્વીનું ગુરુત્વાકર્ષણ લાગતું બંધ થઇ જાય તોView Solution
- 2$200\, kg$ અને $400\, kg$ નાં બે ઉપગ્રહો $A$ અને $B$ પૃથ્વીને ફરતે અનુક્રમે $600\, km$ અને $1600 \,km$ ઊંચાઈએ પરિક્રમણ કરે છે. જો $T_A$ અને $T_B$ એ અનુક્રમે $A$ અને $B$ નાં આવર્તકાળ હોય તો મૂલ્ય $T_B - T_A =$ ........... હશે.View Solution
[ પૃથ્વીની ત્રિજ્યા $=6400\,km$, પૃથ્વીનું દળ $=6 \times 10^{24}\, kg$ ]
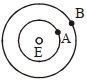
- 3View Solutionનીચેનામાથી ક્યૂ વિધાન સાચું છે : ભ્રમણ કરતાં ઉપગ્રહ માં રહેલા અવકાશયાત્રી નું ઓછું વજન એ પરિસ્થિતી
- 4જો પૃથ્વી સૂર્યની ફરતે ઉપવલય કક્ષામાં સરેરાશ $9.3 \times {10^7}\,m$ ની ત્રિજ્યામાં $1$ વર્ષના આવર્તકાળ મુજબ ફરે છે, જો તેના પર બીજું કોઈ બાહ્ય બળ નો લાગતું હોય તો નીચેનામાથી શું સાચું છે.View Solution
- 5ગ્રહ પર વાતાવરણ એ માત્ર જ્યારે જ શક્ય છે જો (જ્યાં $v_{ rms }$ એ ગ્રહ પરનાં અણુઓની $v_e$ ઝડપ અને $v_e$ એ તે ની સપાટી પરની નિષ્કમણ ઝડપ)View Solution
- 6પૃથ્વી (પૃથ્વીનું દળ $M_E$ અને પૃથ્વીની ત્રિજયા $R_E$) ફરતે $3R_E$ ત્રિજયાના $m$ દળનો એક ઉપગ્રહ વર્તુળાકાર કક્ષામાં છે. આ ઉપગ્રહને $9R_E$ ત્રિજયાની કક્ષામાં લઈ જવા માટે વધારાની કેટલી ઊર્જાની જરૂરી પડે?View Solution
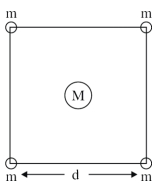
- 7$m$ દળ ધરાવતા ચાર ગોળાઓ $d$ બાજુ (આકૃતિમાં દર્શાવ્યા અનુસાર)નું ચોરસ બનાવે છે. એક પાંચમો $M$ દળ ધરાવતી ગોળો ચોરસના કેન્દ્ર આગળ મૂકવામાં આવે છે. તંત્રની કુલ સ્તિથિ ઊર્જા ........... થશે.View Solution
- 8$R$ ત્રિજ્યા ના ગ્રહ પર એક પદાર્થ ને ઉપરની દિશામાં તેની નિષ્ક્રમણ ઝડપથી અડધી ઝડપે ફેકવામાં આવે તો તેણે પ્રાપ્ત કરેલી મહતમ ઊંચાઈ ?View Solution
- 9એક પદાર્થને નિષ્કમણ વેગ $\left(v_e\right)$ કરતાં $n$ ગણા વેગ સાથે ફેંકવામાં આવે છે. ખુબ જ દૂરનાં અંતરે પદાર્થનો વેગ એે શું હશે ?View Solution
- 10$1\, kg$ ખાંડની ખરીદી ક્યાં સસ્તી પડેView Solution
