${M}$ દળ ધરાવતો પદાર્થ ${V}_{0}$ વેગથી સ્થિર રહેલા $m$ દળના પદાર્થ સાથે સ્થિતિસ્થાપક સંઘાત અનુભવે છે. સંઘાત પછી બંને પદાર્થ શરૂઆતની દિશા સાથે $\theta_{1}$ અને $\theta_{2}$ ખૂણે ગતિ કરે છે. $\theta_{1}$ અને $\theta_{2}$ સમાન કરવા માટે ${M} / {m}$ ના ગુણોત્તરનું મહત્તમ શક્ય મૂલ્ય કેટલું હશે?
JEE MAIN 2021, Diffcult
c
given \(\theta_{1}=\theta_{2}=\theta\)
given \(\theta_{1}=\theta_{2}=\theta\)
from momentum conservation
in \(x\)-direction \(M V_{0}=M V_{1} \cos \theta+m V_{2} \cos \theta\)
in \({y}\)-direction \(0={MV}_{1} \sin \theta-{m} {V}_{2} \sin \theta\)
Solving above equations
\({V}_{2}=\frac{{MV}_{1}}{{m}}, {V}_{0}=2 {V}_{1} \cos \theta\)
From energy conservation
\(\frac{1}{2} {MV}_{0}^{2}=\frac{1}{2} {MV}_{1}^{2}+\frac{1}{2} {MV}_{2}^{2}\)
Substituting value of \({V}_{2} \& {V}_{0}\), we will get
\(\frac{{M}}{{m}}+1=4 \cos ^{2} \theta \leq 4\)
\(\frac{{M}}{{m}} \leq 3\)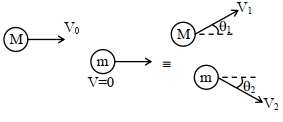
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10kg$ ના સ્થિર પદાર્થ પર $4 N$ અને $3N$ ના પરસ્પર લંબ બળો લાગતાં હોય,તો $10 sec$ પછી ગતિઊર્જા કેટલા ............. $\mathrm{J}$ થાય?View Solution
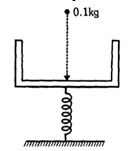
- 2દળ રહિત પ્લેટફોર્મનેે આકૃતિમાં દર્શાવ્યા હલકી સ્થિતિ સ્થાપક સ્પ્રિંગ પર મૂકેલું છે. જ્યારે $0.1\; kg $ દળનો વેગ કણ $0.24 \;m$ ની ઉંચાઈએથી પડતા સ્પ્રિંગમાં $0.01\; m $ નું સંકોચન થાય છે. ............... $\mathrm{m}$ ઉંચાઈએથી કણ પડતાં $0.04\; m$ નું સંકોચન થશે ?View Solution
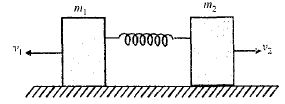
- 3કોઈ સ્પ્રિંગ ને સમક્ષિતિજ ઘર્ષણ રહિત સપાટી પર આકૃતિમાં બતાવ્યા પ્રમાણે બે $m_1$ અને $m_2$ દળ ધરાવતા બે બ્લોક ની વચ્ચે સંકોચન કરવવામાં આવે છે. જ્યારે બ્લોક ને મુક્ત કરવામાં આવે છે, ત્યારે તેનો પ્રારંભિક વેગ $v_1$ and $v_2$ છે. સ્થિર થયા પહેલા બ્લોક દ્વારા કાપેલ અંતર અનુક્રમે $x_1$ અને $x_2$ હોય તો $\left( {\frac{{{x_1}}}{{{x_2}}}} \right)$ નો ગુણોત્તર શું થાય?View Solution
- 4View Solutionમુક્ત પતન કરતા પદાર્થની યાંત્રિક ઊર્જા......
- 5એક પદાર્થ સ્થિર સ્થિતિમાં રહેલાં બીજા સ્થિર પદાર્થ સાથે સ્થિતિ સ્થાપક રીતે ત્રાંસી દિશામાં અથડાય છે. સંઘાત પછી તેઓ એકબીજાને .............. $^o$ ખૂણે ગતિ કરે.View Solution
- 6$M$ દળ અને $v$ વેગ ઝડપે સીધા રસ્તા પર ગતિ કરતાં સાધનનું અટકાયત અંતર ગણો. (( $\mu $ ટાયર અને રસ્તા વચ્ચેનો ઘર્ષણ ગુણાંક છે.)View Solution
- 7એક માણસ સાઇકલ પર સવાર થઇને $7.2 km/hr$ વેગથી જેનો ઢાળ $20m $ અને ઊંચાઇ $1m$ હોય તેવા ઢોળાવ પર ગતિ કરે છે. માણસ અને સાઇકલનું કુલ દળ $100 kg$ છે. માણસનો પાવર કેટલા .....$W$ હશે?View Solution
- 8એક માણસની ગતિઊર્જા તેનાથી અડઘું દળ ઘરાવતા છોકરાથી અડઘી છે.જો માણસની ઝડપમાં $ 1 m/s$ નો વઘારો કરવામાં આવે તો બંનેની ગતિઊર્જા સમાન થાય છે. માણસની મૂળ ઝડપView Solution
- 9$l$ લંબાઈની દોરી ધરાવતાં અને $m$ દ્રવ્યમાન ગોલક ધરાવતા એક સાદા લોલને કોઇ એક નાના કોણ $\theta_0$ થી છોડવામાં આવે છે. ખરબચડી સમક્ષિતિજ સપાટી પર મુકેલ $M$ દ્રવ્યમાનના ચોસલાને તે તેના નિમ્ન બિંદુ પર સ્થિતિસ્થાપક રીતે અથડાય છે. તે પાછો ફેંકાય છે અને કોણ $\theta_1$ સુધી પહોંચે છે, તો $M$ દળ કેટલું હશે?View Solution
- 10એક બોલને $ 20\;m$ ઊંચાઇએથી પ્રારંભિક $v_0 $ વેગથી શિરોલંબ નીચે તરફ ફેંકવામાં આવે છે.આ બોલ પૃથ્વીની સપાટી સાથે અથડાય છે, અથડામણમાં તે $50\%$ ઊર્જા ગુમાવે છે અને તેટલી ઊંચાઇએ પાછો ઊછળે છે. બોલનો પ્રારંભિક વેગ $v_0\;(ms^{-2}$ માં) કેટલો હશે? ($g=10\;ms^{-2}$ લો)View Solution
